Avant de commencer le cours des suites numériques, il est destiné pour les étudiants de : 1er année S et ES ainsi que le Bac Pro
Les suites numériques
- Une suite (un) de nombres réels est une fonction où la variable n est un entier naturel
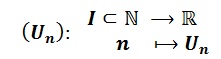
- L’image par la suite (un) d’un entier naturel n est notée Un
- un est le terme général de la suite, n est l’indice du terme un
- (n∈N ) est le rang du terme un
Exemple:
- Soit la suite définie par un = n – 2. Les termes de la suite (un) sont tels que u = -2 ; u1 = -3 ; u2 = 0 ; … ; u20 = 18 ;
- u20 est le terme d’indice 20, c’est le 21e terme de la suite puisque le premier terme est uo. La suite (vn) définie par vn=√(n-4) n’est définie que pour n ≥ 4. On la note (vn)n≥4.
Définitions d’une suite
Suite définie par une formule explicite : un = f(n)
Une suite (un) explicite définie au moyen d’une fonction de variable n un = f(n)
Exemple :
La suite (un) définie pour ∀n∈N par :
Un=f(n)=√n.
Un=f(n)=1/(n+1)
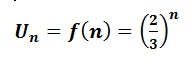
Suite définie par récurrence
Une suite (un) définie au moyen d’une relation de récurrence un+1 = f(n) le terme suivant est défini en fonction du terme précédent.
Exemple :
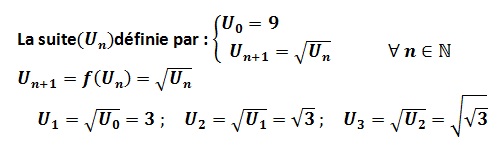
Sens de variation d’une suite
Suite croissante
La suite (un) est croissante si, ∀n∈N U(n+1)≥Un
Exemple de suite croissante
La suite (Un) définie ∀n∈N* par :
Un=√n
Suite décroissante
La suite (Un) est décroissante si, ∀n ∈ N, un (n+1) ≤ un.
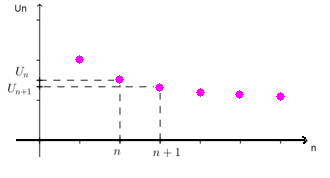
Exemple :
La suite (un) définie ∀n∈N* par :
Un=1+1/n
Suite constante
Définition:
La suite (Un) est constante si, ∀n∈N U(n+1)=un
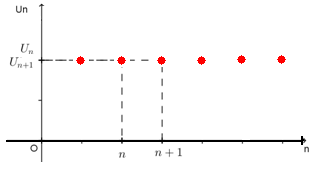
Exemple : La suite (un) définie ∀n∈N par : Un=2
Suite Monotone
Définition:
Une suite (un) est monotone si elle est soit croissante, soit décroissante, soit constante, autrement dit, si elle ne change pas de sens de variation.
Méthodes pour étudier le sens de variation d’une suite
on a 4 méthodes :
1ère méthode
étudier le signe de Un+1 – Un Pour tout entier naturel n.
2ème méthode
Etudier le sens de variation de la fonction f sur [0 ; + ∞ [ Si Un = f(n),
3ème méthode
Comparer U(n+1)/Un si Un>0
Si (∀n∈N) Un > 0 Comparer Un+1/Un
Si U(n+1)/Un > 1 Un est croissant
Si U(n+1)/Un < 1 Un est décroissant
4ème Méthode
Utilisation le raisonnement par récurrence
Etudier le signe de Un+1 – Un pour tout entier naturel n.
1ère Méthode
on étudie le signe de un+1 – un . pour tout entier naturel n
Si un+1 – un ≥0 alors la suite (un) est croissante sur N
Si un+1 – un≤0 alors la suite (un) est décroissante sur N
Exemple:
Etudier le sens de variation de la suite (un) définie ∀n∈N* par:
Un=2-2/n
Réponse:
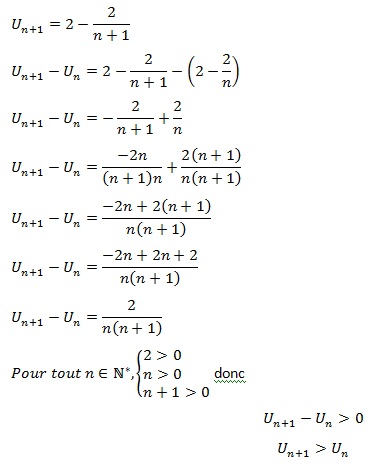
Conclusion:
La suite (un) est monotone croissante.
Etudier le sens de variation de la fonction f sur [0 ; + ∞[ Si Un = f(n)
2ème Méthode:
Cas où un = f(n)Si la suite est définie au moyen d’une fonction de variable , alors le sens de variation de la suite est semblable à celui de la fonction
Etudier le sens de variation de la fonction f sur [0 ; + ∞[
Exemple:
Etudier le sens de variation de la suite (Un) définie ∀nℕ∗ par:
Un= 2 – 2/n
Réponse:
Un = f (n) en posant f la fonction définie sur ]0 ; +∞[ par f(x)= 2- 2/x
f est dérivables sur ]0 ; +∞[
f’ (x)=-2×-1/x²
f’ (x)= 2/x²
∀ x ∈]0 ; +∞[, f’ (x) > 0 donc la fonction f’ est croissante
Conclusion:
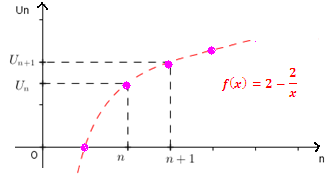
La suite (un) est monotone croissante
Comparer Un+1/ Un Si Un > 0
Si ( ∀ n ∈ N ) Un > 0 Comparer Un+1 / Un Si Un+1 / Un > 1 Un est croissant
Si Un+1 / Un < 1 Un est décroissant
Exemple:
Etudier le sens de variation de la suite :
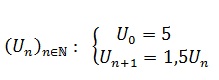
On montre d’abord que: (∀n∈N) Un > 0
Soit la proposition P(n) : Un>0 ∀n∈N
- Initialisation : Montrons que P(n) est vraie pour n=0 Sachons que U0 = 5 Donc U0 > 0 La proposition P(n) est vraie pour n=0.
- Hérédité : On suppose que la proposition P(n) soit vraie pour un entier k≥0 , c’est à dire qu’on suppose que Uk > 0 . Montrons qu’alors P(n) est vraie pour l’entier k + 1 c’est à dire que U(k+1)>0. D’après de la suite donnée on a : U(k+1) = 1,5 Uk En utilisant l’hypothèse de récurrence on a Uk > 0 1,5 X Uk > 0 D’où U(k+1) >0
Conclusion : la proposition P(n) : Un>0 est vraie pour ∀n∈ N

On a démontré précédemment que ∀ n∈ N Un>0 donc on a :
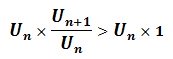
on multiplie les deux membres d’une inégalité par un réel strictement positif
U(n+1)>Un ∀n∈N
Conclusion : La suite (Un ) est monotone croissante
4ème méthode
Utilisation du raisonnement par récurrence
Pour utiliser la récurrence, on doit d’abord conjecturer le sens de variation.
Exemple :
Etudier le sens de variation de la suite (un)définie pour tout entier naturel n par :
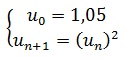
Réponse :
Démonstration par récurrence du sens de variation
Soit la proposition : P(n):u(n+1)>un ∀ n∈N
- Initialisation : Montrons que P(n) est vraie pour n=0 .
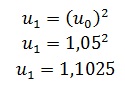
Donc u1>u0 La proposition P(n) est vraie pour n=0.
Hérédité : On suppose que la proposition P(n)soit vraie pour un entier k≥0 , c’est à dire qu’on suppose que u(k+1)>uk.
Montrons qu’alors P(n) est vraie pour k+1, c’est à dire que u(k+1+1)>u(k+1)
u(k+2)>u(k+1)
En utilisant l’hypothèse de récurrence, on a : u(k+1)>uk
Or la fonction carrée est strictement croissante sur [0 ; +∞[ et puisque Un>0 ∀n∈N,
Alors u(k+1) )^2>(uk )^2
D’où u(k+2)>u(k+1)
Conclusion : la proposition P(n) : u(n+1)>un, est vraie pour ∀ n ∈ N
Conclusion : La suite (vn ) est monotone croissante.
Exercice: Pour ∀n∈N, on donne la suite (Un) définie par : U_N=n^2-5n+3
Démontrer que la suite (Un) est croissante à partir d’un certain rang.
Réponse:
On calcule la différence : U n+1 – Un
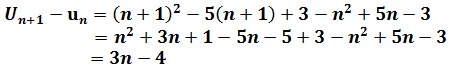
ensuite on étudie le signe de : U(n+1) – Un = 3n – 4
pour 3n-4 donc pour n≥1,3 Ainsi pour n≥2 on a. U(n+1)-Un≥0
On en déduit qu’à partir du rang 2, la suite Un est croissante
Exercice:
Pour ∀n∈N, on donne la suite (un) définie par:
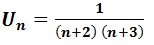
Démontrer que la suite (un) est décroissante.
Réponse:
(n+2) (n+3)>0 ∀n∈N donc Un>0
Un > 0
Calculons le rapport : U(n+1)/ Un
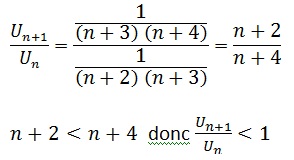
On en déduit que (Un ) est décroissante.
Suites majorées, minorées, bornées
Suites majorées
Définition : La suite Un est majorée si : ∃ M∈R/ ∀ n∈N: Un≤M.
Exemple 1:
Montrer que la suite ( Un ) définie pour tout n∈N* par :
Un = 4 – 4/n
est majorée par M= 4 et tracer sa courbe
Réponse:
On calcule Un- 4 puis on étudie son signe :
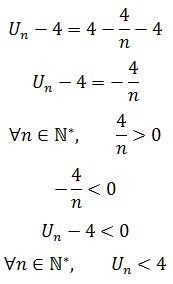
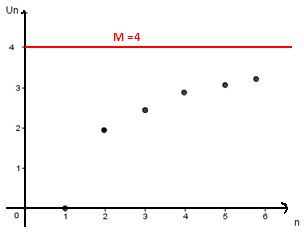
Conclusion :La suite (Un) est majorée par 4
Utiliser un raisonnement par récurrence.
Exemple 2:
Soit la suite (un) définie sur N par :
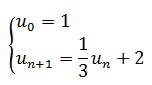
Démontrer que cette suite est majorée par 3
Réponse:
Utilisons le raisonnement par récurrence
Une suite est majorée par 3 si ∀ n∈ N un≤3
raisonnement par récurrence :
Soit la proposition P(n): un≤3, ∀ n∈N.
Initialisation : Montrons que P(n) est vraie pour n=0 .
On sait que u0 = 1 donc u0 ≤ 3 La proposition P(n) est vraie pour n=0.
Hérédité : On suppose que la proposition P(n) soit vraie pour un entier k≥0 , c’est à dire uk ≤ 3.
Montrons alors que P(n) est vraie pour l’entier k+1, c’est à dire que u(k+1)≤3
On cherche à écrire une inégalité concernant Uk+1 en partant de l’hypothèse de récurrence : Uk ≤ 3.
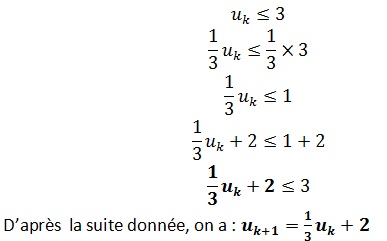
Donc u(k+1) ≤ 3
Conclusion : la proposition P(n) : ∀n∈N,un≤3 est vraie.(un ) est majorée par 3.
Suites minorées
Définition: La suite Un est minorée si : ∃ m∈R/∀ n∈N:un≥m
Exemple:
Montrer que la suite (Un)définie pour tout n ∈ N par :
Un=3+1/(2+n)
est minorée par m= 3 et tracer sa courbe
Réponse: On calcule Un – 3 puis on étudie son signe :
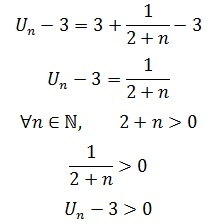
∀n∈N, Un > 3
Conclusion : La suite Un est minorée par 3
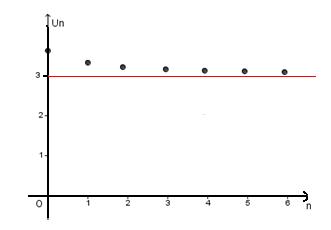
Suites bornées
Définition: La suite (Un ) est bornée si ∃ m,M ∀ n∈N: m≤un≤M
Une suite à la fois majorée et minorée est bornée.
Exemple:
Montrer que la suite (Un) définie pour tout n∈N par
Un=2+ sinn est bornée et tracer sa courbe
Réponse:
On part de l’encadrement de sin(n) puis on arrive à un encadrement de Un.
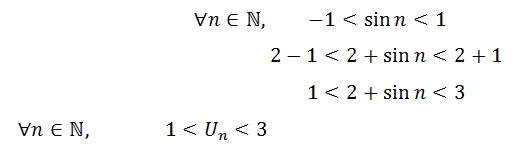
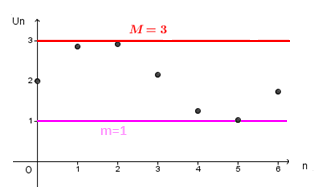
Conclusion: La suite ( Un ) est bornée par 1 et 3
Limite d’une suite
Limite finie
Définition:
Soit l un réel. On dit que la suite ( un ) a pour limite l quand n tend vers +∞ signifie que tout intervalle ouvert contenant l contient tous les termes de la suite à partir d’un certain rang. On écrit alors
lim(n→+∞)Un = 1
Exemple:
La suite (Un )n ∈ N^* définie par Un=1+1/(n+2) a pour limite l=1.
lim (n→+∞) Un = 1
Limite infinie
Définition:
Dire qu’une suite (Un ) a pour limite +∞ quand n tend vers +∞ signifie que tout intervalle ]A ;+∞ [ , avec A réel , contient tous les termes de la suite à partir d’un certain rang.
Exemple:
La suite (Un )(n ∈ N) définie par Un=n² a pour limite +∞.
Cela signifie que tout intervalle ]30 ; +∞[ contient tous les termes de la suite ( U6,U7…) à partir d’un certain rang n0 ( n0 = 6 ).
Pas de limite
Exemple 1:
La suite (Un )(n ∈ N) définie par Un=(-1)^n prend deux valeurs -1 et 1 . Cette suite n’a pas de limite.
Exemple 2:
La suite (Un)(n ∈ N) définie par Un=cos(n) prend alternativement des valeurs réelles entre -1 et 1..
Cette suite n’a pas de limite.
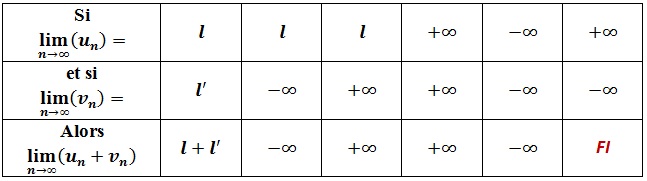
Théorèmes généraux sur les limites de suites
Operations sur les limites de suites
Somme:
Exemple:
Déterminer lim(n→+∞)(3n+√2n)
Réponse:
lim (n→+∞) (3n)=+∞ et lim(n→+∞) (√2n) =+∞ donc, par somme, lim(n→+∞)(3n+√2n)=+∞
Produit:
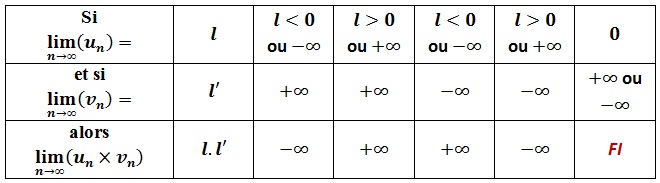
Exemple: Déterminer lim(n→+∞)n√n
Réponse:
lim(n→+∞)(n)=+∞ et lim(n→+∞) (√n)= +∞ donc, par produit, lim(n→+∞)(n√n)=+∞
Quotient:
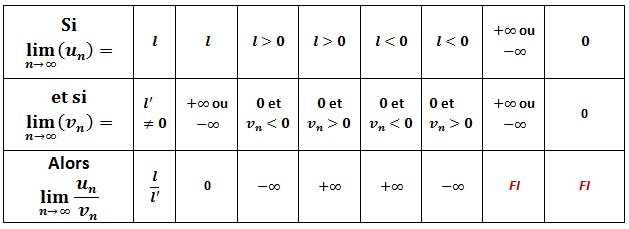
Exemple:
Déterminer lim(n→+∞) 3/n
Réponse:
lim(n→+∞)(3)=3 et lim(n→+∞)(n)=+∞ donc , lim(n→+∞) 3/n=0
Cas d’indétermination
Il y a 4 cas d’indétermination ∞-∞ ;0×∞ ; ∞/∞ ; 0/0
Dans ces cas, on est obligé de modifier l’écriture de Un.
Exemple:
Déterminer lim(n→+∞)(n-√n).
Réponse:
On a lim(n→+∞)(n)=+∞ et lim(n→+∞)(√n)=+∞ donc (n-√n ) forme indéterminée ∞ – ∞
On modifie l’écriture de n-√n, par factorisation de l’expression :
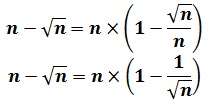
la limite de chaque facteur :
lim(n→+∞)n=+∞ et lim(n→+∞)(1-1/√n)=1
Donc, par produit :
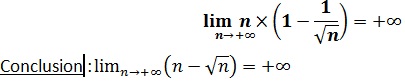
Limite d’une suite définie par une fonction polynôme
La limite d’une fonction polynôme à l’infini est égale à la limite en l’infini de son monôme de plus haut degré. Il en est donc de même pour une suite définie par une fonction polynôme.
Exemple:
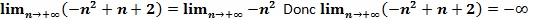
Limite en l’infini d’une suite définie par une fonction rationnelle
La limite en l’infini d’une fonction rationnelle est égale à la limite du quotient de ses monômes de plus haut degré. Il en est donc de même pour une suite définie par une fonction rationnelle. Une fonction rationnelle est une fonction de la forme
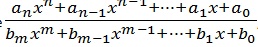
où
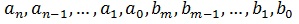
sont des réels et net m des entiers naturels tels que an≠0 et bm≠0.
Exemple:
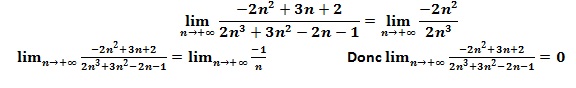
Limites et convergences
Des théorèmes pour calculer la limite d’une suite
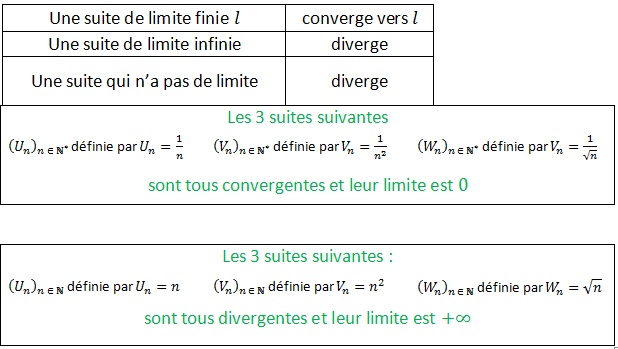
Théorèmes de comparaison
1ère théorème
Soient (un) et (vn) deux suites telles que, à partir d’un certain rang , un≤vn.

Exemple:
Etudier la convergence de la suite (Vn) définie pour tout n∈N par Vn=n^2+(-1)^n
Réponse :

2ème théorème
Soit (un) et (vn) deux suites telles que, à partir d’un certain rang , un≤vn.
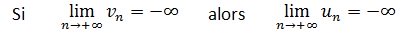
Etudier la convergence de la suite(Un) définie pour tout entier naturel n par Un=-n^2+cos(n)
Réponse:
On définit la suite (Vn ) pour tout entier naturel n par Vn=-n^2+1
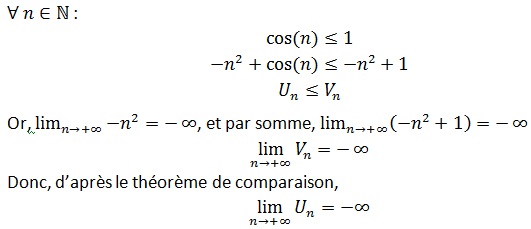
Théorème des gendarmes ou l’encadrement
Soit (un), (vn)et (wn)trois suites telles que, à partir d’un certain rang , vn≤un≤wn.
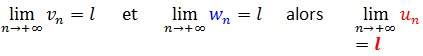
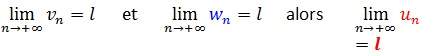
Exemple:
Etudier la convergence de la suite (Vn) définie pour tout entier naturel n non nul par :
Un = (sin(n))/n+2
Réponse :
On définit la suite (Un ) pour tout entier naturel n non nul par :
Vn=-1/n+2
et la suite (Wn ) pour tout entier naturel n non nul par :
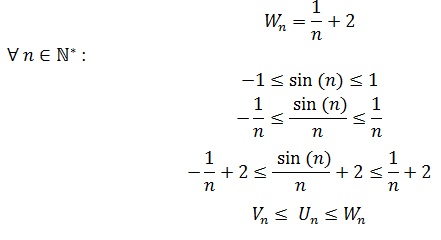
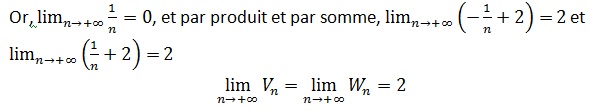
Donc, d’après le théorème des gendarmes,
lim(n→+∞)Un=2
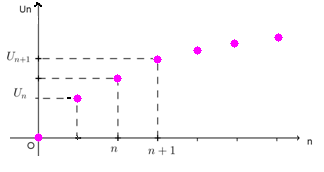
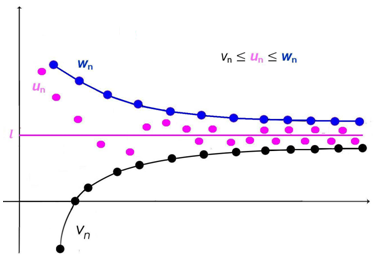
Illustration graphique :
Remarque
( un )converge vers l <=>(u(n+1) ) converge vers l .
Soit (un ) une suite définie pour tout n∈N par u(n+1)= f(un )
Si la suite ( un ) converge vers une limite finie l, alors l vérifie l’équation l=f(l)
Démonstration :
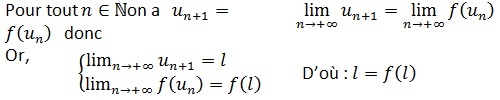
Théorème de la convergence d’une suite monotone
Soit une suite croissante. Si cette suite est majorée alors elle converge.
Exemple:
La suite (Un) définie sur N* par Un=2-1/n
On montre que :
(Un) est croissante
(Un) est majorée par 2
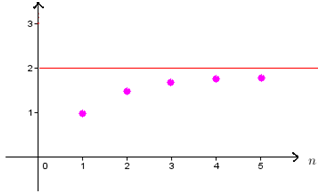
On conclut que d’après le théorème de la convergence d’une suite monotone, la suite (Un) a une limite finie.
Soit une suite décroissante. Si cette suite est minorée alors elle converge.
Exemple:
La suite (Vn) définie sur N^* par Vn=2+1/n
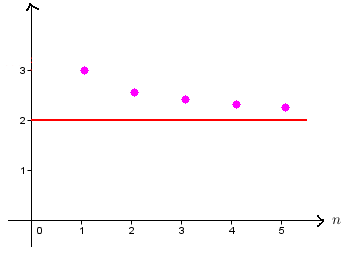
On montre que :
(Vn) est décroissante
(Vn) est minorée par 2 ( par exemple)
On conclut que d’après le théorème de la convergence monotone, la suite (Vn) a une limite finie.
Propriété : Suite croissante de limite l
Soit une suite croissante. Si cette suite est converge vers l alors l est un majorant de la suite.
Exemple:
La suite (Un) définie sur N* par Un=2-1/n
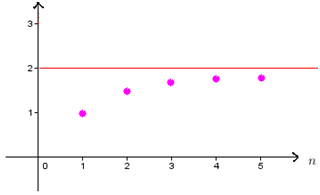
On montre que :
(Un) est croissante.
(Un) converge vers 2.
On conclut que 2 est un majorant de la suite (Un).
Théorème : suite croissante non majorée
Soit une suite croissante. Si cette suite n’est pas majorée, alors elle diverge vers +∞.
Si vous avez besoin de quelques choses à propos de ce cours ( suites numériques ), l’équipe Coursuniversel à votre disposition.








Reflection tres poussee et bien structure.
J’adore,le cour est très bien détaillé.
Je vous souhaite un agréable futur, je fais mon mieux pour les élèves et les étudiants(e) africains(e).