Cours précis de la continuité d’une fonction pour le terminale S et ES.

Vous Trouverez Tous les cours du Mathématique ICI

Continuité  en un Point

Soit une fonction f(x)  définie sur un intervalle  I ouvert et  x₀  un élément de I   On dit que la  fonction  f(x) est continue en x₀  si et seulement si :

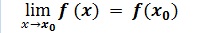
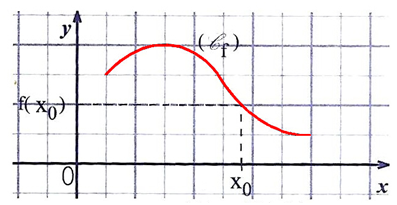
f(x) est continue en x₀ 

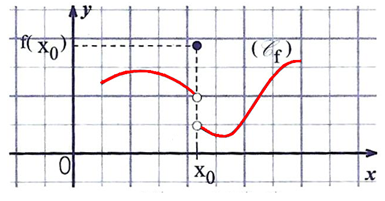
f(x) n’est continue pas  en x₀ 

Maintenant en passe a la :

Continuité à droite, continuité à gauche

Continuité à droite

Soit une fonction définie sur  [x₀  , x₀+ α[  tel que α >0  

On dit qu’une fonction est continue à droite  en x₀ si :

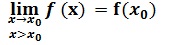
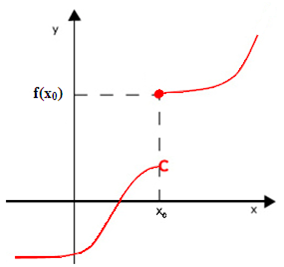
Continuité à gauche

Soit une fonction définie sur    ]x₀-α, x₀ ]   tel que α >0  

On dit qu’une fonction est continue à gauche  en x₀ si 

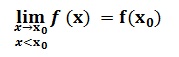
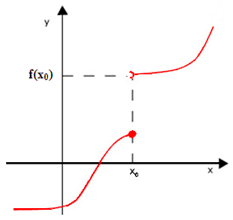
Continuité  sur un intervalle

On dit qu’une fonction f (x) est continue sur un intervalle I si elle est continue en tout point de cet intervalle.

Graphiquement

f (x) est continue sur I si on tracer sa courbe représentative sans lever le crayon.

Exemple:

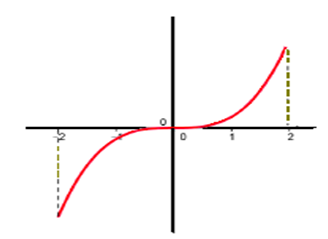
𝑓 est une fonction définie sur l’intervalle I = [ – 2 ; 2 ]

Cette courbe se trace sans lever le crayon sur I donc la fonction 𝑓 est continue sur:  I= [ – 2 ; 2 ].

Exemple :  Discontinuité  sur un intervalle

f présente une ‘discontinuité’ en x₀, si f n’est pas continue en x₀.

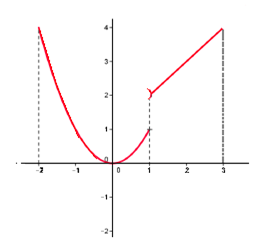
f  est une fonction définie sur l’intervalle I = [– 2 ; 3]

sa courbe ne peut pas être tracée sans lever le crayon au point d’abscisse 1 donc la fonction f   

 n’ est pas continue sur I = [– 2 ; 3].

(par contre elle est continue sur les intervalles [– 2 ;1] et ]1 ; 3])

Operations des fonctions   continues

Soit I un intervalle  inclus dans ℝ     et  k un nombre réel

Si  f et g  deux fonctions continue sur I   alors :

 k f  ,    f+ g  , f x g   sont des fonctions   continues sur I  

  Si  f et g  deux fonctions continue sur I   et g  ≠0 sur I   alors : 

f/g et 1/g sont des fonctions   continues sur I  

La Continuité des fonctions Usuels

Toutes les fonctions suivantes sont continues sur leur domaine de définition :

– polynomiales

– rationnelles

– racines

– trigonométriques

– exponentielles

– logarithmes

Voici des Exemples:

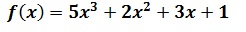
La fonction est une fonction polynôme (à coefficients réels), définie et continue sur IR

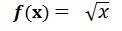
la fonction racine carrée, définie et continue sur   IR+

f(x)= cos x  La fonction cosinus est définie et continue sur   IR

f(x)= sin x La fonction sinus  est définie et continue sur   IR

f(x)= I x I = la fonction est définie et continue sur   IR

Continuité d’une fonction composée

La composée des fonctions f et g o f est la fonction g o f 😡 => g(f(x)).

Soit f et g  deux fonctions numériques

Si f est  continue en x₀  et si  g est continue en f(x₀) alors gof est continue en x₀.

Si f est continue sur I et si  g est continue en tout point de f(I) alors gof est continue sur I.

Continuité d’une fonction exercices corrigés

Voici quelques exercices de la part de : Coursuniversel

Soit la fonction définie sur  R+*  par    :

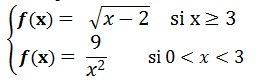
Montrer que  f est continue en 3.

Situation 1

f est continue en 3 si

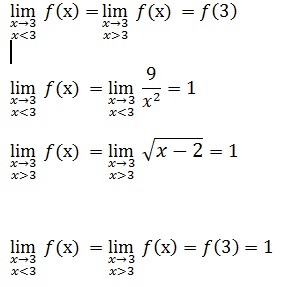
donc la fonction est continue en 3.

Exercice 2

Calculer la valeur de “k” pour que f(x) soit continue en x=1

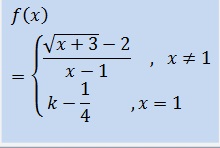
SOLUTION:

f est continue en 1 si

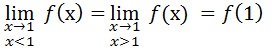
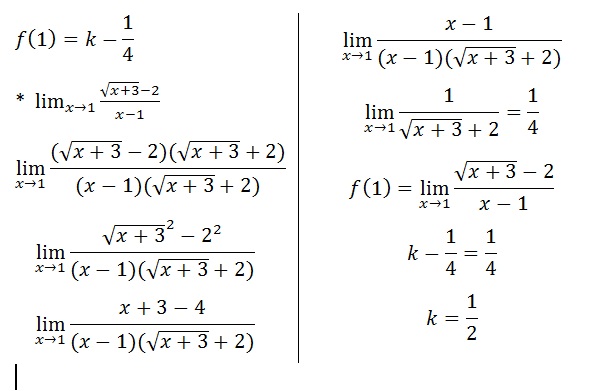
Exercice 3

Montrer que:

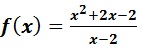
est continue en x = 1

Solution

f est continue en 1 si

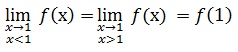
f (-1) = -1

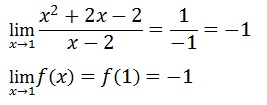
Donc f(x) est continue en x = 1

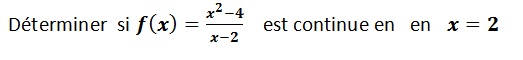
Solution:

f(2) = 0/0 f(x) non définie en x=2

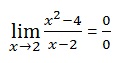
factoriser  pour  éliminer l’indétermination:

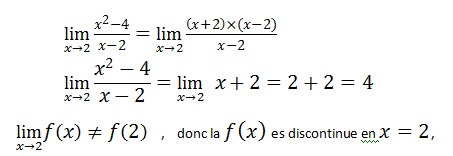
L’image d’un intervalle d’une fonction continu

L’image d’un intervalle I de IR  par une fonction f continue sut I est un intervalle de IR

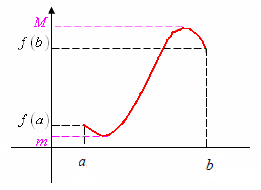
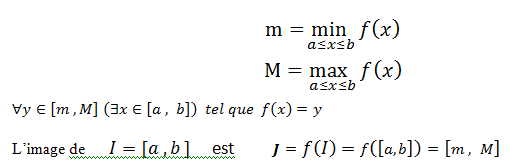
L’image d’un segment [a, b] par une fonction continue f est un segment [m, M]

L’image d’un intervalle d’une fonction continu monotone  strictement  croissante

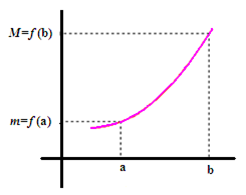
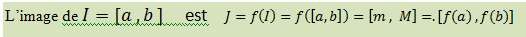
L’image d’un intervalle d’une fonction continu monotone    strictement  décroissante

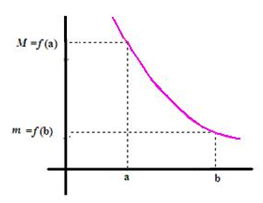
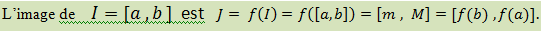
Voir Aussi : La théorème des valeurs intermédiaires

Partagez ce cours avec vos ami(e)s.

Si vous avez une question concernant la continuité d’une fonction, mettez le au commentaire.