Le cours des théorème des valeurs intermédiaires avec les exercices corrigés destiné pour les étudiants du terminale s et es ainsi que les étudiants du lycée.

Le théorème

Soit une fonction continue sur un intervalle I   et   a, b deux  réels de  l’intervalle de   I

Pour tout réel k compris entre f (a) et f (b), il existe au moins un réel c  appartenant à [a, b] tel que f (c) = k.

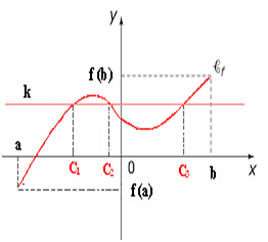
 Voir la courbe :

La fonction de la courbe est  continue sur:

 l’ intervalle I =  [a, b]

La valeur C n’est pas  unique : f (c₁) =  f (c₂) =  f (c₃) = k

Conséquence :

Si f une fonction continue sur l’intervalle [a ; b] 

et si f(a) × f(b) < 0

Alors

 l’équation f(x) = 0  a au moins une solution sur l’intervalle [a ; b]

Voir la Courbe

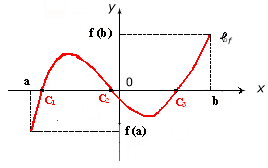
La fonction est continue sur l’ intervalle I =  [a, b]

 f(a) × f(b) < 0 alors :

les solutions  de l’équation f(x) = 0  x= c₁ ,  x= c_2,  x=  c₃ 

Fonction continue  et strictement monotone

Vocabulaire : Fonction monotone est une fonction soit croissant ou décroissant

Théorème

Si une fonction f est continue et strictement monotone sur un intervalle [a ; b]   alors pour tout réel k compris entre f(a) et f(b), il existe un unique réel c compris entre a et b tel que f(c) = k.

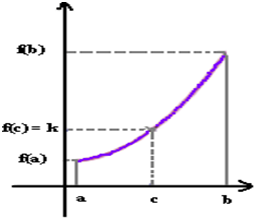
Si f est croissant   f (a) £  k £ f (b)

L’image de I par f        

Si f est  décroissant   f (b) £  k £ f (a)

L’image de I par f        

Les Exercices corrigés de la théorème des valeurs intermédiaires.

Exercice 1

Soit la fonction définie sur par x3-x²-x+1

1) Montrer que la fonction f  est continue sur [-1 ;2].

2) Calculer  f(-1)  et  f(2)

3) En déduire que l’équation f(x) = 5    admet au moins une solution dans [-1 ; 2].

Corrigé

La fonction f est une fonction polynôme, donc elle est continue sur ℝ et en particulier Sur 

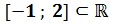
2)  on calcule        f(-1) =1   et      f(2)=10

3) Montrons que l’équation f(x) = 5     admet au moins une solution dans l’intervalle [-1 ; 2].

D’une part, f est continue sur l’intervalle [-1 ; 2]. D’autre part, comme

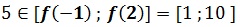
 Le théorème des valeurs intermédiaires permet d’affirmer que l’équation f(x) = 5       admet au moins une solution dans [-1 ; 2].

Exercice 2

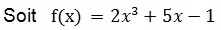
1. Justifier que f est continue sur R

2. Calculer f(0) et f(1).

3. En utilisant le TVI montrer qu’il existe x0 ∈ [0, 1] tel que f(x0) = 0.

Corrigé 2

1. La fonction f est un polynôme,  donc  F(x) est Continue sur IR

2. f(0) = −1  et f(1) = 6 

3. La fonction f est continue sur  [0, 1] et  f(0) x f(1) <0,   

donc , par le TVI, il existe x0 ∈ [0, 1] tel que f(x0) = 0.

Exercice 3

Soit f   la fonction définie sur

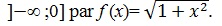
Montrer que l’équation f (x)=2 admet une unique solution dans ]-∞, 0]

Corrigé 3

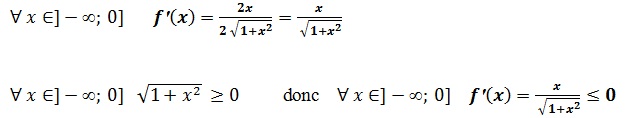
donc   f  est strictement décroissante sur   ]-∞, 0]

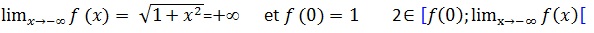
D’Après  le théorème des valeurs intermédiaires, on déduit que l’équation :

F(x) = 2 Admet une solution unique dans ]-∞, 0]

Et Finalement:

Pour toute incompréhension , laissez votre commentaire ci-dessous

CoursUniversel vous répondrai le plutôt possible

Le format PDF du cours sera disponible bientôt.

Voir aussi : Continuité d’une fonction