Cours Probabilités

Voici le cours probabilités simple et précis pour les étudiants de : Terminale et Bac.

Expérience aléatoire

Univers, issues et événements

Aléatoire = imprévisible ; lié au hasard.

le lancer d’un dé est une expérience aléatoire, car on ne peut pas prévoir avec certitude quel en sera le résultat, puisque ce dernier est imprévisible « lié au hasard ».
le résultat d’une expérience aléatoire est appelé issue
L’ensemble formé de toutes les issues possibles de l’expérience aléatoire est appelé univers noté Ω (Oméga),
Un événement est une partie de l’univers, formée d’une ou de plusieurs issues possibles
Les sous-ensembles de l’univers Ω sont appelés événements.
Un événement élémentaire est une partie de l’univers Ω, formée d’une seule issue possible
On appelle événement impossible, un événement qui ne contient aucun des éléments de Ω. Il lui correspond la partie vide Ø de Ω.
On appelle, événement certain, l’ensemble Ω de toutes les possibilités. Il lui correspond la partie pleine de Ω
On appelle, événements incompatibles, deux parties disjointes de Ω

Exemple 1.

Lancer un dé à 6 faces et noter le chiffre apparent sur la face supérieure , il indiquera l’une des six issues suivantes : 1, 2, 3, 4, 5 ou 6.

- - Il y a 6 issues possibles ;
  - L’univers de l’expérience est Ω={1 ; 2 ; 3 ; 4 ; 5 ; 6 } ;
  - A = « le résultat est pair » est un événement; A={2 ; 4 ; 6 } .
  - B = »le résultat est impair » est un événement: B = {1, 3, 5}.
  - C = « le résultat ≥ 6 » est un événement élémentaire C={6 } ensemble qui contient une seule issue.

Exemple 2.

Lancer une pièce de monnaie à 2 faces « Pile » ou « Face » et noter la face exposée, est une expérience aléatoire :
Il n’y a que 2 issues possibles
L’univers de l’expérience est Ω={P ; F } ; A={P} et B={F } sont des événements élémentaires

Exemple 3.

Dans une urne avec 1 boule blanche et deux boules noires,
– le tirage d’une boule : Ω = { B, N },
– le tirage successif de deux boules avec remise :Ω = { (B, B), (B, N), (N, B), (N, N)},
– le tirage successif de deux boules sans remise : Ω = { (B, N), (N, B), (N, N) },

Voir aussi: Limites de Fonctions ( Cours et Exercices )

Opérations sur les événements

Intersection de deux événements.

On considère deux événements A et B , l‘intersection des événements A et B est un événement qui est noté A∩ B « A et B » qui est réalisé si et seulement si, A est réalisé et B est réalisé simultanément.

Exemple
on lance un dé à six faces on appelle :A l’évènement « obtenir un nombre impair »

B l’évènement « obtenir un nombre pair »
C l’évènement « obtenir un nombre ≥ 3
- L’évènement A ={1 ;3 ;5}
- L’évènement B = {2 ;4 ;6}
- L’évènement C = {3 ;4 ;5 ;6}
- L’évènement A∩C = {3 ;5}.
- L’évènement B∩C = {4 ;6}.
- L’évènement A∩B =Ø

Réunion de deux évènements

On appelle réunion des deux événements A et B noté A∪ B, l’événement « A ou B » qui est réalisé si et seulement si A est réalisé ou B est réalisé

Exemple

Reprenons l’expérience précédente :
- L’évènement A ={1 ;3 ;5}
- L’évènement B = {2 ;4 ;6}
- L’évènement C = {3 ;4 ;5 ;6}
- L’évènement A∪B = {1 ;2 ;3 ;4 ;5 ;6}.

Complémentaire

L’événement complémentaire de B , que l’on note $\bar{B}$ « non B » correspond à l’événement $\bar{B}$ ={1, 3, 5}

Loi de probabilité

Définition

Dans une expérience aléatoire qui comporte un nombre fini d’issues appelé univers: Ω= {ω₁ ; ω₂ ; ω₃ ; … ; ω_n } est un ensemble fini

On définit une loi de probabilité sur tel que: pour tout i, 0 ≤ p_i ≤ 1 p_i est la probabilité élémentaire de l’événement {ω_i} et on note pi = P({ωi }) parfois plus simplement p(ω_i).

La somme des probabilités de tous les événements élémentaires :

Si Ω= {ω₁ ; ω₂ ; ω₃ ; … ; ω_n } alors P(ω₁ ) + P(ω₂ ) + … + P(ω_n ) = 1.

Équiprobabilité

Définition

Dans une expérience aléatoire, il y a équiprobabilité si tous les événements élémentaires d’un univers ont la même probabilité d’être réalisés.

Théorème

S’il y a équiprobabilité pour une expérience dont l’univers Ω comporte un nombre total « n » événements élémentaires, alors la probabilité de chaque événement élémentaire est égale à $\frac{1}{n}$

Exemple

si on lance un dé , l’univers de l’expérience aléatoire est :

Voir aussi: Primitive D'une Fonction ( Cours & Exercices )

Ω={1 ; 2 ; 3 ; 4 ; 5 ; 6} ; les six faces ont exactement la même chance d’apparaître.

Par conséquent, la probabilité de l’apparition de chaque face est de $\frac{1}{6}$

La loi de probabilité du lancer d’un dé équilibré est donnée par : pour tout ω∈ Ω P({ω})= $\frac{1}{6}$

On écrit la loi de probabilité dans un tableau :

issues	1	2	3	4	5	6	Total
P({ω})	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	1

P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1

Cardinal

Définition

Si A est un ensemble fini, on appelle cardinal de A le nombre d’éléments dans A , on note card(A)

Théorème

Si un évènement A de cet univers Ω comporte k évènement élémentaires alors P(A)= $\frac{k}{n}$
Puisque : card(A) = k et card (Ω)=n

La probabilité de l’événement A peut s’écrire de cette manière :

$P(A)=\frac{Nombre d ' issues favorables}{Nombre d ' issues possibles}=\frac{card(A)}{card(\Omega Ω)}=\frac{k}{n}$

Probabilité d’une réunion

Théorème

Dans une expérience aléatoire, on considère deux événements A et B.

Si A et B sont deux événements quelconques, alors :

P(A∪B) = P(A) + P(B) – P(A∩ B)

Si A et B sont incompatibles c’est-à-dire A∩B =Ø , alors :

P(A ∪ B) = P(A) + P(B)

Probabilité conditionnelle

Définition

On considère une expérience aléatoire, A et B sont deux événements avec p(A)≠0 La probabilité de B, sachant que A est réalisé, est notée P_A(B) $P_{A}(B)=\frac{P(A\cap B)}{P(A)}$

Exemple :

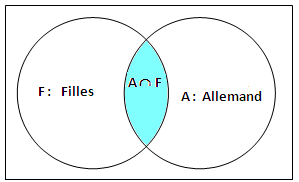
Dans un lycée, les 250 élèves (150 Filles, 100 garçons) qui étudient une seconde langue Allemand ou Espagnol : dont on connait 30 filles qui étudient la langue Allemand
- Calculer P_F(A)
On considère les événements :
- A : « l’élève étudie l’Allemand »
- F: « l’élève est une fille ».

Utilisation du diagramme

$P_{F}(A)=\frac{P(A\cap F)}{P(F)}$

$P(A\cap F)=\frac{30}{250}=\frac{3}{25}$

$P(F)=\frac{150}{250}=\frac{3}{5}$

$P_{F}(A)=\frac{P(A\cap F)}{P(F)}$

$P_{F}(A)=\frac{P(A\cap F)}{P(F)}=\frac{3}{25}\times \frac{5}{3}=\frac{1}{5}$

Utilisation d’un arbre pondéré

Exemple :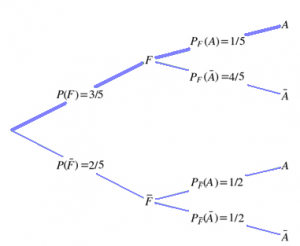

$P(\bar{F})=1-P(F)$

$P(\bar{F})=1-\frac{3}{5}=\frac{2}{5}$

Explication d’ un arbre pondéré

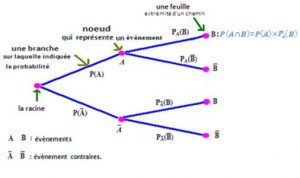
Propriétés :

La somme des probabilités des branches issues d’un même nœud est égal : P(A) + P(A) =1
La probabilité d’une « feuille » « extrémité d’un chemin » est égale au produit des probabilités du chemin aboutissant à cette feuille :P(A)x P_A(B)

Indépendance de deux événements

Deux événements sont indépendants lorsque la probabilité de l’un ne dépend pas de la réalisation de l’autre, soit : P_A(B)=P(B)

Deux événements sont indépendants lorsque P(A∩B)= P(A)×P(B)