Je vous présente le cours précis et simple de : la dérivée d’une fonction avec des exercices corrigés pour tous les niveaux et spécialement : Bac Pro, S et ES.

Dérivé en un point

Soit f une fonction définie sur un intervalle I et x un élément de I

On dit que la fonction f est dérivable en x si et seulement si  :

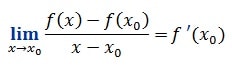
Ou bien

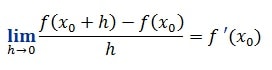
f´( x) est le nombre dérivé de la fonction f en x.

Interprétation géométrique

L’équation tagente de la courbe de f

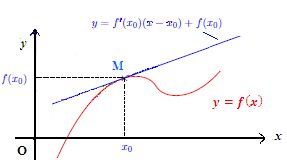
Théorème : Si la fonction f est dérivable en x alors la courbe de f admet au point M(x ; f(x)) une tangente dont l’équation est :

y = f'( x ) .(x – x ) + f( x )

f'( x ) est le coefficient directeur de la droite tangente à la courbe de f

Exemple :

La fonction f est définie par  : f(x)= 2x²+1

Déterminons l’équation de la tangente en x = 1

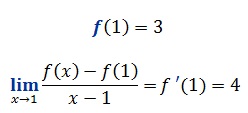
L’équation de la tangente y = f’ ( x ).(x – x )+ f( x ) = 4(x-1)+3=4x-1

Dérivabilité à droite, dérivabilité à gauche:

Dérivabilité à droite

f est dérivable à droite en x si et seulement si :

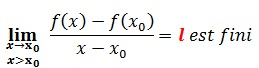
Dérivabilité à gauche

  f est dérivable à gauche en x si et seulement si : 

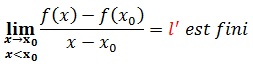
 le nombre dérivé à gauche au point x0  et on note : 

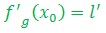
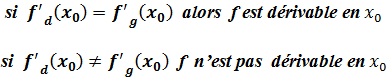
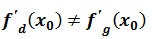
f n’est pas dérivable en x mais elle est dérivable à droite et à gauche en x .

la courbe de f admet une demi-tangente à droite et une demi tangente à gauche en x

et A( x ; f(x) ) est un point anguleux , les deux demi tangentes ne sont pas portées par la même droite.

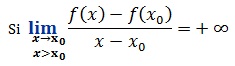
Alors la courbe (C ) admet à droite au point A( x ,f( x )) a une demi tangente verticale dirigée vers le haut

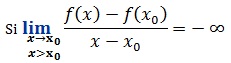
Alors la courbe (C ) admet à droite au point A( x ; f(x ) a une demi tangente verticale dirigée vers le bas

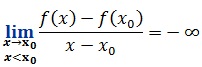
Alors la courbe (C ) admet à gauche au point A( x ,f( x )) a une demi tangente verticale dirigée vers le haut

Exemples

Etudier la dérivabilité de la fonction f définie par f(x)=|x| en 0

Solution

∀ x ∈ [0 ; +∞ [ f(x) = x

∀ x ∈ ] -∞ ; 0 ] f(x) = -x

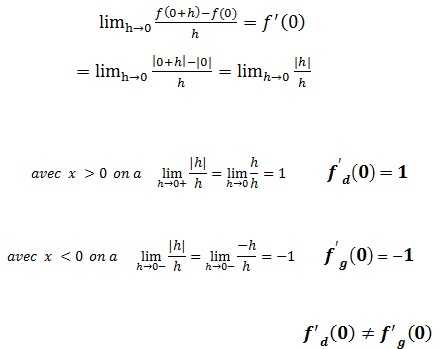
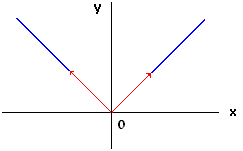
la courbe de f admet une demi-tangente à droite et une demi tangente à gauche en .

A( 0, f(0) ) est un point anguleux.

Etudier la dérivabilité de la fonction f définie par : f(x)=√x en 0

Solution

La fonction f est définie sur [0;+∞ [

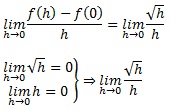
Est une forme indéterminée

On change  la forme

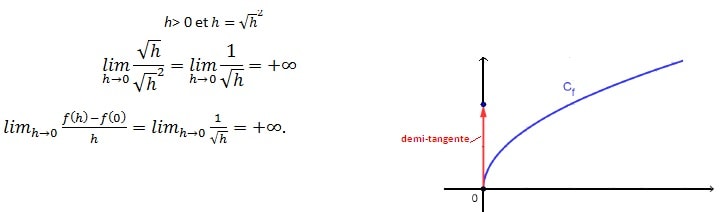
La fonction f n’est pas dérivable en 0

f admet une demi-tangente verticale  dirigée vers le haut en 0.

---

 Dérivabilité en -2 de la fonction f définie par

Etudier la dérivabilité de la fonction f définie par : f(x)=|x+2| en -2

La fonction f est définie sur R

Si x+2>0 alors f(x)=x+2

Si x+2<0 alors f(x)=-x-2

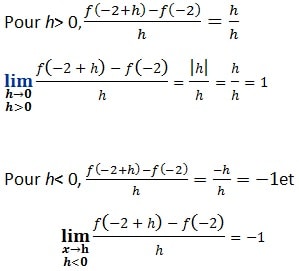
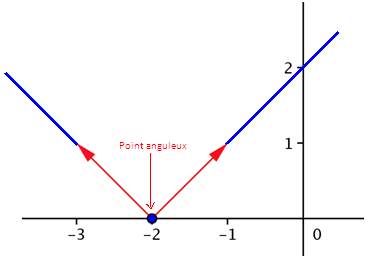
f n’est pas dérivable en -2 mais elle est dérivable à droite et à gauche. Sa courbe admet  une demi-tangente à droite et une demi tangente à gauche en -2.

A(-2,f(-2) ) est un point anguleux.

Fonction dérivée sur un Intervalle

f’: x ↦ f'(x)

f   fonction définie sur un intervalle I.

On dit que f est dérivable sur I si elle est dérivable ∀ x∈I.

La fonction f’ est appelée   fonction dérivée de la fonction f  

On la note f’ la fonction dérivée de f telle que : f’: x↦f'(x)

Ecriture différentielle f’ (x)=df/dx

Exemple

Déterminer la  dérivée de la fonction : f(x)=3x² + 4x – 5

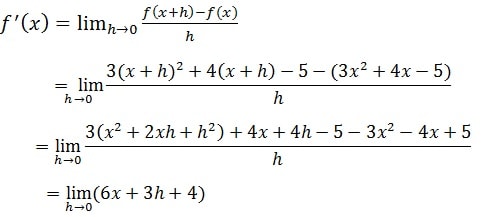
Finalement f'(x)=6x+4

Opérations sur les dérivées

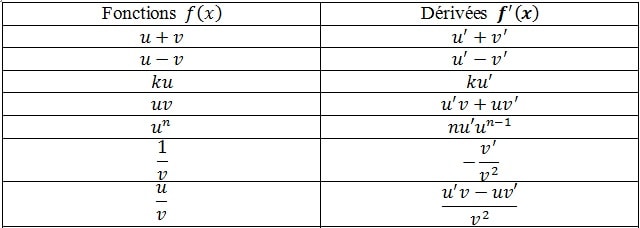
Dérivées des fonctions usuelles

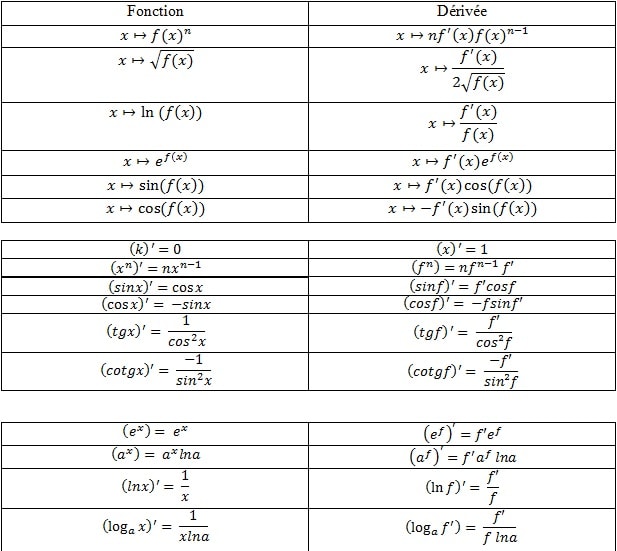
Dérivée de fonctions composées

Dérivée de la composition de deux fonctions

Soient f et g  deux fonctions définies  respectivement sur  I  et  f (I).

Si  f  est dérivable sur I  et g est dérivable sur f (I).

Alors la dérivée de la fonction composée g ∘ f  est dérivable sur I:

∀x ϵ I ( g∘ f)’(x)=g’(f(x)). f’(x)

Dérivée et sens de variation

L’étude des variations d’une fonction

Théorème  :

Soit f une fonction dérivable sur I.

∀x ∈ I, f ‘(x) <0 alors f est strictement décroissante sur I.

∀x ∈ I, f ‘(x) >0 alors f est strictement croissante sur I.

∀x ∈ I, f ‘(x) =0 alors f est constante sur I.

Extremum d’une fonction

Théorème

Soit f une fonction dérivable sur I. Soit x ∈ I.

Si f ( x ) est un extrémum alors f ‘( x )=0

Si f ‘ s’annule en x en changeant de signe alors f ( x ) est un extrémum.

Exercices Corrigés : Fonction dérivée

Exercice 1

Soit f(x)= k (constante)

et f’ (x)=0

Déterminer la dérivé de :

f(x) = 20 => f’ (x) = 0

f(x)= – 20 => f’ (x) = 0

Exercice 2:

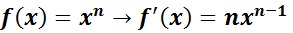
Déterminer la dérivé de :

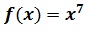
on appliquant la fonction ci-dessus, voici le résultat du dérivé:

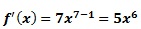
Exercice 3:

soit la fonction suivante

f(x) = g(x) ∙ h(x) f’ (x)=g’ (x) ∙ h(x) + g(x) ∙ h(x)

Déterminer la dérivé de :

f(x)= (5x-7) * (2x+9)

On appliquant la formule ci-dessus:

f’ (x) = 5(2x+9) + 2(5x-7) = 10x+45+10x-14 = 20x+31

Déterminer la dérivé de :

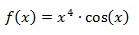
On appliquant la formule dérivée ci-dessus

Voici le résultat :

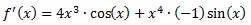
Exercice 5:

f(x) = h( g(x) )

et f’ (x) = h'(g(x)) ∙ g'(x)

Déterminer la dérivé de :

f(x)= sin ⁡(3x²-1)

Nous obtenons :

f’ (x)= cos ⁡(3x²-1) ∙ 6x

Lire Aussi : Nombres complexes

Et finalement on a arrivé à la fin du cours, si vous avez des questions ou des notes, lissez le dans le commentaire, l’équipe de COURSUNIVERSEL va vous répondrai le plutôt possible.