Voici un cours de : Primitive d’une fonction pour les étudiants du baccalauréat ( Terminale S et ES ) avec des exercices corrigés

Définition

Soit f une fonction définie sur un intervalle I.

Une primitive de f sur I est une fonction F dérivable sur I telle que telle que F ‘(x) = f (x)

Exemple:

Primitive de la fonction f(x)=2x est F(x)=x²+C où C est une constante réelle.

Théorème: Toute fonction continue sur un intervalle I admet des primitives sur I

Théorème: Soit f une fonction continue sur un intervalle I et F une primitive de f sur I

Toute primitive de f sur I est de la forme F∶ x → F(x)+C où C est une constante réelle

Opérations sur les primitives

Propriété

Si F est une primitive de f sur I et si G est une primitive de g sur I alors:

F + G      est une primitive de f + g sur I

∀ k ∈ R , kF est une primitive de k f sur I

∫f(x)dx = F(x) + C

Déterminer les primitives sur IR de   f(x)=  3x²

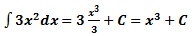
∫ [f(x)± g(x) ± h(x) ± …. = ∫ f(x) dx ± ∫ g(x)dx  ± ∫ h(x)dx  ±…

On passe vers les exercices corrigés : Primitives d’une fonction

Exemple 1:

Primitive de : (5x² +6x – 10)

L’étape 1: ∫ (5x²+6x-10) dx = ∫ 5x² dx + ∫ 6x dx – ∫ 10 dx

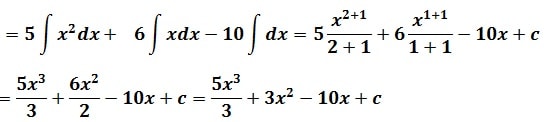
Voici le deuxième exercice corrigé

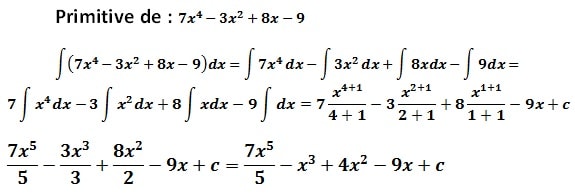
Voici le troisième Exercice

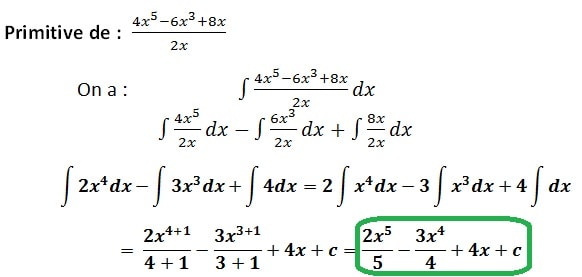
Voici un autre exemple

Calcul de primitives :

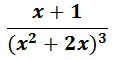
Correction:

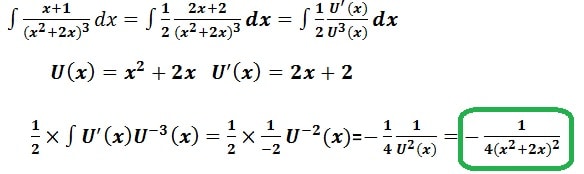
Exercice Calcul de primitives :

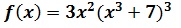
Correction :

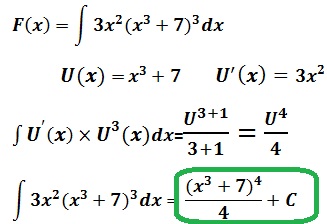
Exercice : En segmentant la fonction

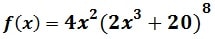
Voici le corrigé :

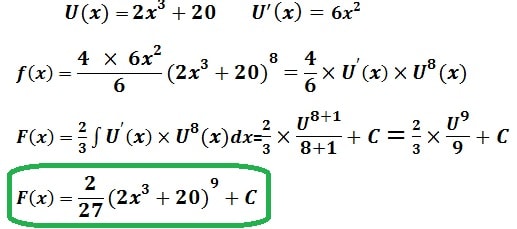
Intégration par parties

∫ U V’ = U V – ∫ U’ V

Calcul de primitives de :

ln⁡|x|

On Applique le primitive : ∫ ln⁡|x| dx

U= ln ⁡|x| V’=1 U’= 1/x V=x

∫ U V’ = ∫ 1 × ln⁡|x| ∫ U’ V= ∫ 1/x × x=x U V=x × ln⁡|x|

Intégration par parties

∫ U V ‘ = U V – ∫ U’ V

∫ ln⁡ |x| dx= x × ln⁡|x|-x + C

Voici des exemples corrigés :

On Calcul le primitives de : x ln⁡|x|

On a : ∫ x ln⁡ |x| dx

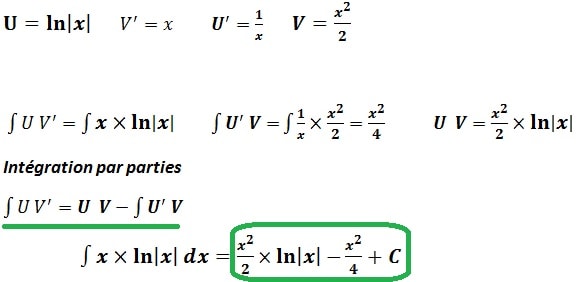
Voici un autre Exemple :

Calcul de primitives de :

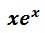
Voici la correction d’exercice :

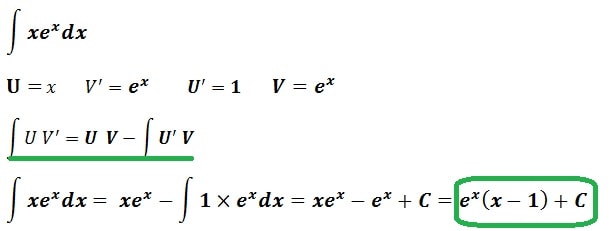
Exercice de calcul des primitives de Sin(x)

Exemple : x² sin⁡x

∫ x² sin ⁡x dx

U =⁡ x² V’ = sin⁡x U’ = 2x V = – cos⁡x

∫ U V’ = U V – ∫ U’ V

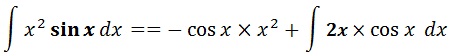
Et en fin, on a arrivé à la fin du cours, Si vous avez des Questions ou des Notes, Laissez nous vos Commentaires