Coursuniversel vous propose un cours simple et précis des nombres complexes pour tout les niveaux ( terminale s , mpsi, ….) avec des exercices corrigés.
On Commence 😉
On appelle le nombre complexe :
Tout nombre s’écrit sous la forme z = x+ i y ( x, y deux nombres réels : x ∈ℝ et y ∈ℝ) et i un nombre imaginaire qui vérifie i² = – 1
L’ensemble des nombres complexes est noté ℂ ℂ= { x+ i y / (x ; y) ∈ℝ² }
Tel que i² = -1
Ecriture algébrique d’un nombre complexe
Tout nombre complexe z s’écrit d’une manière unique sous la forme :
z = x+ i y, où x et y sont deux nombres réels.
Ecriture z = x+ i y est la forme algébrique du nombre complexe z
x est la partie réelle de z noté : x = Re(z) ;
y est la partie imaginaire de z noté: y = Im(z).
Egalité de deux nombres complexes
Deux nombres complexes z et z’ son égaux si et seulement si :
ils ont la même partie réelle et la même partie imaginaire.
z = x+ i y et z’ = x ‘+ i y ‘
z = z’ ⇔ Re(z) = Re(z’) et Im(z) = Im(z’)
x+ i y = x ‘+ i y ‘ ⇔ x= x ‘ et y = y ‘
Soit z un nombre complexe, alors :
[ x+ i y = 0 ⇔ x = 0 et y = 0 ]
Opérations sur les nombres complexes
Tous les règles de calcul dans ℝ addition , multiplication s’applique aussi dans ℂ sans oublier i² = – 1
Par conséquent ℂ constitue une extension algébrique de ℝ.
Soit deux nombres complexes z = x+ i y et z’ = x ‘+ i y ‘
où x et y sont deux nombres réels et k nombre réel
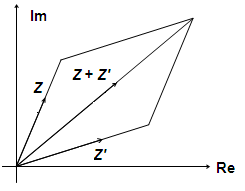
La somme de z et z’ est : z+z ‘= (x+x ‘ )+i(y+y ‘).
Le produit de z et z’ est défini par : z z ‘=( x x ‘ – y y ‘)+i (x y ‘+ y x ‘ )
Soit z et z’ deux nombres complexes , sous algébrique avec z≠0
L’inverse de z ≠0 est :
(x+ i y) (x- i y) =x²+y²
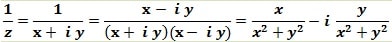
Le quotient de z ‘ par z ≠0 est :
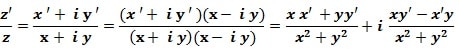
Exemple 1:
(a+bi)² = (a+bi) (a+bi) = a²+abi+abi+(bi)² = a²+2ab i- b²
(a-bi)² = (a-bi) (a-bi) = a² – abi – abi + (bi)² = a² – 2abi – b²
(a+ bi) (a – bi) = a² – abi + abi – (bi)² = a² + b²
Exemple 2 :
Calculer sous forme algébrique (3+4i)/(5+2i)
Réponse
(3+4i)/(5+2i) = (3+4i)/(5+2i) × (5-2i)/(5-2i)
= (23+14i)/(25+4) = 23/29+14/29 i
Conjugué d’un nombre complexe
Définition
Soit z = x+ i y un nombre complexe où x et y sont deux nombres réels
Le nombre complexe x- i y s’appelle le conjugué de z on le note : z ̅
z ̅=x- i y
Le conjugué de z ̅ est : z ̿ =z
zz ̅=x² +y²
z+ z ̅=2Re(z) z – z ̅=2i Im(z)
z est un nombre réel si et seulement si z=z ̅
z est un imaginaire pur si et seulement si z ̅=−z
Opérations sur le conjugué des nombres complexes
Soit z et z’ deux nombres complexes, alors
(z+z’) ̅=z ̅+z ̅’
(z×z’) ̅=z ̅×z ̅’
z ≠0
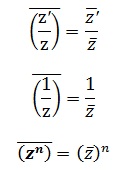
Voici quelques exercices :
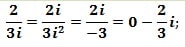
et

Représentation géométrique d’un nombre complexe
Le plan P muni d’un repère orthonormé direct ( O , u ⃗ , v ⃗ )
x et y deux nombres réels
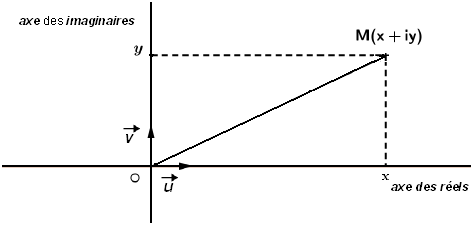
A tout nombre complexe z = x + i y , on associe le point M de coordonnées (x ; y) dans le repère orthonormé direct ( O , u ⃗ , v ⃗ )
On dit que :
- le point M est l’image du nombre complexe z. on l’écrit M(z)
- (OM) ⃗ est le vecteur image du nombre complexe z on l’écrit OM(z)
Affixe d’un point
A tout point M(x ; y) du plan P on associe le nombre complexe z = x + i y on dit que
z est l’affixe du point M on la note zM
Affixe d’un vecteur
Le plan complexe est muni d’un repère orthonormé direct ( O , u ⃗ , v ⃗ )
Définition
A tout vecteur W de coordonnées (x , y) , on associe le nombre complexe z = x + i y.
z s’appelle l’affixe du vecteur W
Théorème
Si M et M’ deux points dans un même repère orthonormé, leurs affixes sont respectivement 𝒛𝑴 et 𝒛M’ alors l’affixe du vecteur (MM’) ⃗ est égal à 𝒛M’−𝒛𝑴 : Affixe (MM’) ⃗ )= 𝒛M’−𝒛𝑴
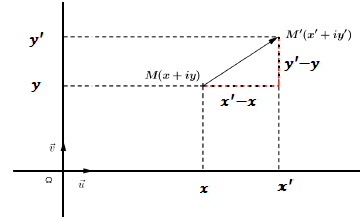
Explication :
𝑧𝑀=𝑥+𝑖𝑦 a pour coordonnée M (𝑥 ;y)
𝑧𝑀′=𝑥′+𝑖𝑦′ a pour coordonnée M’ (𝑥′ ; 𝑦′)
Donc le vecteur (MM’) ⃗ a pour coordonnées (𝑥′−𝑥 ; 𝑦′−𝑦)
Donc , par définition, l’affixe de (MM’) ⃗ est (𝑥′−𝑥) + 𝑖 (𝑦′−𝑦) = 𝒛M’−𝒛𝑴
Exemple :
Soit A d’affixe zA = -3 + 2i et B d’affixe zB = 3 + 4i
Alors l’affixe de AB ⃗ est: zB – zA = (3 + 4i) – (-3 + 2i) = 3 + 4i + 3 – 2i = 6 + 2i
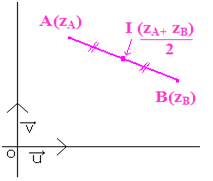
Affixe du milieu d’un segment
Si I est le milieu du segment [AB]
Alors:
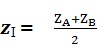
Module d’un nombre complexe
Définition
Soit 𝒛 = x+ i y un nombre complexe non nul, x et y sont deux nombres réels
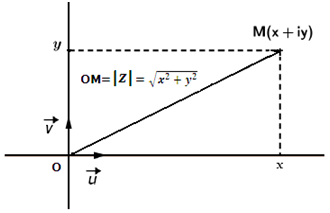
Le module de 𝒛 noté |𝒛|, est la longueur OM
C’est-à-Dire:
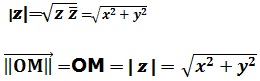
Théorème
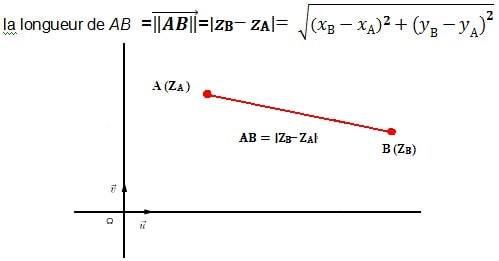
soit les points A et B ont pour affixes 𝑧A et𝑧B alors
A (𝑧A ) a pour coordonnée A (𝑥A ; yA)
B(𝑧B ) a pour coordonnée B (𝑥B ; yB)
Exemple :
Soit A d’affixe zA = -3 + 2i et B d’affixe zB = 3 + 4i
Alors l’affixe de AB ⃗ est : zB – zA = (3 + 4i) – (-3 + 2i) = 3 + 4i + 3 – 2i = 6 + 2i
Exemple :
La distance AB de l’exemple précédent est :
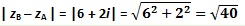
Opérations sur le module des nombres complexes
Soit z et z’ deux nombres complexes
|z×z’|=|z|×|z’|
|z ̅ |=|-z|=|z|
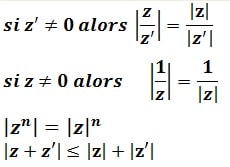
Argument d’un nombre complexe
Soit 𝒛 un nombre complexe non nul et M son image sur le plan complexe d’un repère orthonormé direct ( O , u ⃗ , v ⃗ )
On appelle l’argument de z est une des mesures,
de l’angle orienté
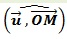
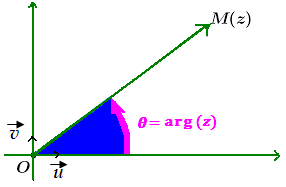
On le noté 𝐚𝐫𝐠 (𝒛) exprimée en radian, on l’écrit :
𝐚𝐫𝐠 (𝒛) ≡ ( u ⃗, (OM) ⃗ ) [2π] ≡ 𝜽 [2π]= 𝜽+2kπ k∈ℤ
Théorème
Soit un nombre complexe non nul
𝐚𝐫𝐠 (-z ) ≡ π+𝐚𝐫𝐠 (𝒛) [2π]
𝐚𝐫𝐠 (z ̅ ) ≡ – 𝐚𝐫𝐠 (𝒛) [2π]
Operations sur Argument des nombres complexes
Soit 𝒛 et 𝒛′ deux nombres complexes non nul
𝐚𝐫𝐠 (𝒛 x 𝒛′)≡ 𝐚𝐫𝐠 (𝒛)+𝐚𝐫𝐠 (𝒛′) [2π]
𝒂𝒓𝒈 ( 1/z ) ≡ −𝐚𝐫𝐠 (𝒛) [2π]
𝒂𝒓𝒈 (z/z’ ) ≡ 𝐚𝐫𝐠 (𝒛)−𝐚𝐫𝐠 (𝒛′) [2π]
𝒂𝒓𝒈 (z^n) ≡ n 𝐚𝐫𝐠 (𝒛) [2π] n ∈ℤ
Exemple :
Soit A d’affixe zA = 2 + 5i et B d’affixe zB = 3 + 4i
L’affixe de AB est : zB – zA = (3 + 4i) – (2 + 5i) = 3 + 4i – 2 – 5i = 1 – i
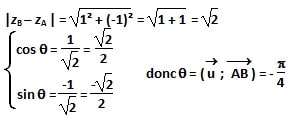
Forme trigonométrique d’un nombre complexe
Définition
Tout nombre complexe z non nul peut s’écrire sous la forme :
𝒛= 𝒓 (𝒄𝒐𝒔𝜽+𝒊𝒔𝒊𝒏𝜽) où 𝒓=|𝒛| et 𝜽≡ 𝐚𝐫𝐠 (𝒛) [2π]
Cette écriture s’appelle forme trigonométrique de 𝒛
Théorème
Soit 𝒛 un nombre complexe non nul
Si 𝒛= r (𝒄𝒐𝒔𝜽+𝒊𝒔𝒊𝒏𝜽) et r>0 donc |𝒛| = 𝒓 et 𝐚𝐫𝐠 (𝒛) = 𝜽 [2π]
Egalités de deux nombres complexes écrits sous forme trigonométrique
Soit deux nombres complexes 𝒛 et 𝒛’ non nuls
𝒛 = 𝒛’ ⇔ ( |𝒛| =|𝒛’ | et 𝐚𝐫𝐠 (𝒛) ≡ 𝐚𝐫𝐠 (𝒛’) [2π] ).
Relation entre la forme algébrique et trigonométrique d’un nombre complexe
Théorème
Soit z un nombre complexe non nul on peut l’écrire sous deux formes :
Soit z = r (𝒄𝒐𝒔𝜽+𝒊𝒔𝒊𝒏𝜽) forme trigonométrique
z = x + i y forme algébrique
On a :
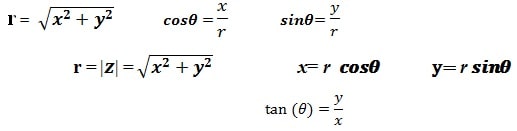
Voici des applications numériques
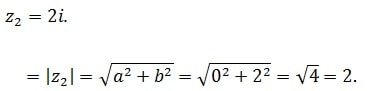
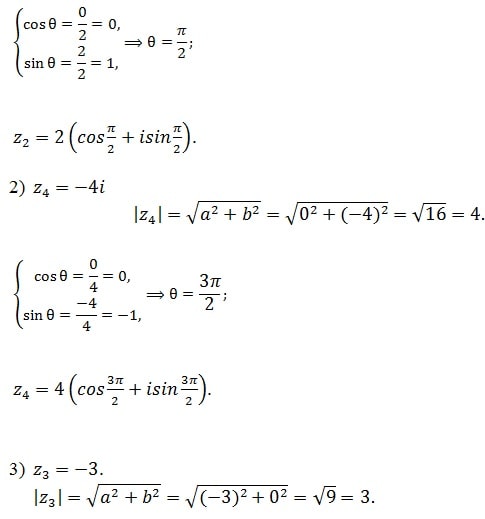
Application à la géométrie
On considère quatre points distincts A, B, C, d’affixes respectives zA, zB , zC .

Angle orienté
Pour tous points A, B, C et D d’affixes respectives zA, zB , zC, zC tels que (A≠B) et (C≠D), on a :
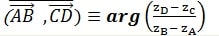
Colinéarité et orthogonalité
Propriété 3 :
Alignement de 3 points distincts ou parallélisme de deux droites
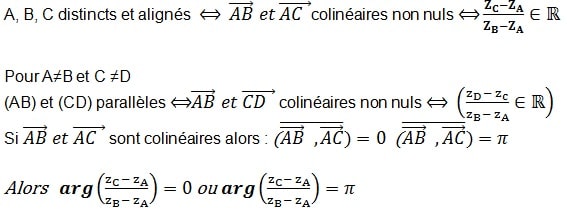
Propriété 4 : orthogonalité
Pour montrer l’orthogonalité de deux droites. Pour A≠B et C ≠D
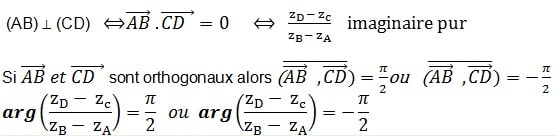
Donc
Les trois points A, B, C d’affixes respectives zA, zB , zC
A, B et C sont alignés si et seulement si :
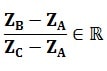
Nature d’un triangle
Pour montrer qu’un triangle ABC est :
Isocèle en A : AB = AC ⇔ |zB − zA| = |zC − zA|
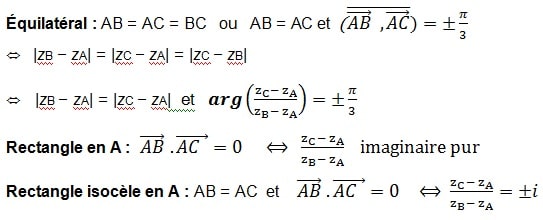
Ecriture complexe d’une translation
Soit M(z) un point du plan d’affixe z et u un vecteur quelconque du plan.
M’ c’est l’image du point M par la translation t de vecteur u

Ecriture complexe d’une homothétie
Dans le plan complexe d’un repère orthonormé direct ( O ,u , v)
Soient deux points distincts M(z) d’affixe z et Ω(ω) d’affixe ω
M’ est l’image du point M par l’homothétie h de centre Ω et de rapport k.
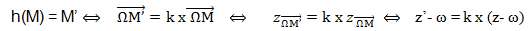
L’écriture complexe de l’homothétie h de centre Ω d’affixe ω , et de rapport k est :
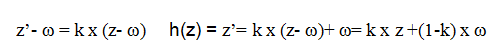
Expression complexe d’une rotation
Dans le plan complexe d’un repère orthonormé direct ( O, u, v )
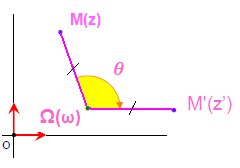
Soient deux points distincts M(z) d’affixe z et Ω(ω) d’affixe ω
M’ est l’image du point M par rotation r de centre Ω et d’angle 𝜽.

Expression complexe d’une symétrie centrale
M’ est l’image du point M par la symétrie S de centre Ω cela signifie que Ω est le milieu du segment [MM’],
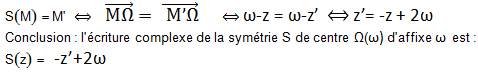
Notation d’un nombre complexe exponentielle
Tout nombre complexe non nul z de module r et d’argument 𝜽 peut s’écrire sous forme exponentielle
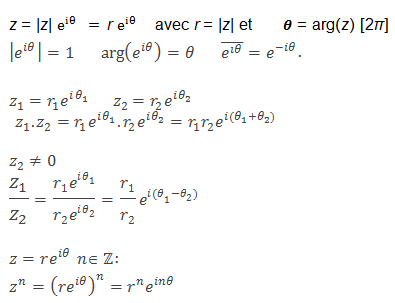
Lire aussi : primitive d’une fonction








1 réflexion au sujet de « Nombres complexes : Cours et Exercices Corrigés »