Cours : Circuit RLC pour les étudiants en Terminale, Bac, Université ( Deug )

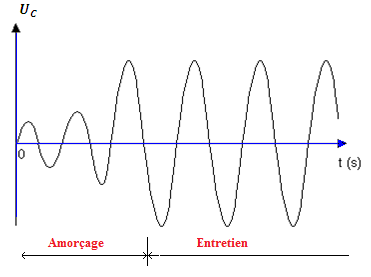
Décharge oscillante d’un condensateur dans une bobine

 Observation d’oscillation électrique

Activité 1

Suivre l’évolution de la tension aux bornes d’un condensateur chargé, branché aux bornes d’une bobine.

On constitue un circuit RLC en associant en série :

• un rhéostat de résistance ajustable r’ 

• un condensateur de capacité C 

• une bobine d’inductance L  de résistance r

La résistance équivalente du montage est notée R = r + r’.

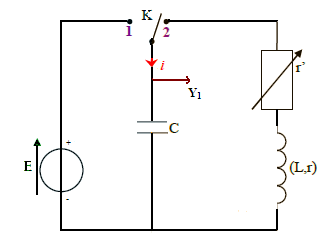
Pour charger le condensateur par le générateur :

Placer L’interrupteur (K) en position 1,

 Lorsque la charge aux bornes du condensateur atteint la tension U_c = E

Basculer L’interrupteur (K) en position 2.

La voie Y₁ est reliée à l’oscilloscope à mémoire,  branché aux bornes du condensateur pour suivre l’évolution de la tension

Vos observations et interprétation sur l’écran de L’oscilloscope ?

Observations et interprétations

L’interrupteur (K) étant sur la position (2), donc on a  un circuit (R,L,C) série où le condensateur se décharge dans le conducteur ohmique et la bobine.
La tension U_c(t) visualisée est alternative, elle diminue puis augmente successivement cela montre que le condensateur se décharge et se recharge  régulièrement : cette décharge est oscillante, elle évolue dans un sens puis dans l’autre.

 L’amplitude des oscillations décroît avec le temps, ces oscillations sont amorties, et aussi libre puisqu’ aucun énergie  de l’extérieur n’est fournit au circuit  donc ce sont des oscillations libres amorties.

Conclusion

La décharge d’un condensateur, dans une bobine d’un circuit (R,L,C) série , entraine l’ apparition des oscillations libres amorties. On dit que le circuit (R,L,C) série est un oscillateur électrique libre amortie .

L’amortissement est  dû à l’énergie dissipée par effet joule dans  la résistance R du circuit ( R = r’ + r).

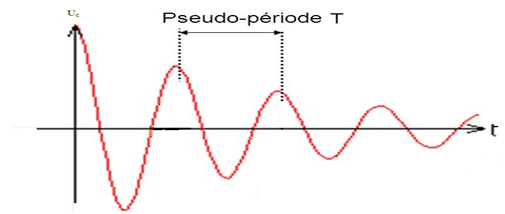
Définition de la pseudo-périodique T :

On appelle pseudo-périodique T, le temps qui s’écoule entre deux valeurs maximales, consécutives de la tension U_c(t).

étude de l’amortissement des oscillations

Activité 2 :  

On reprend  l’activité 1  en  augmentant   les valeurs de  r’ . c.à.d  R= r’+r
Qu’observe-t-on ?

Observations et interprétations

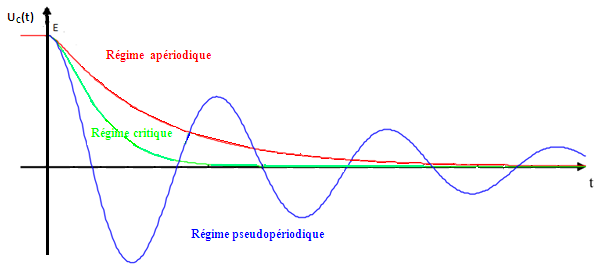
Pour des valeurs faibles de R, on  observe des  oscillations qui durent longtemps dont l’amplitude décroit progressivement : une tension oscillante amortie c’est le régime pseudo-périodique.

Lorsqu’ on augmente la résistance R  l’amortissement est plus important.

Si on augmente encore la résistance R, on arrive à une valeur limite où il n’y a plus d’oscillations Pour des valeurs élevées de R  la tension U_c(t). tend  lentement vers zéro  c’est le régime apériodique.
La valeur de R qui délimite les deux régimes (pseudo-périodique et apériodique) appelée résistance critique on la note R_c   c’est Le régime critique correspond à un amortissement plus important.

Etude du pseudo -période

Activité 3 : 

On est dans l’état  du régime pseudo-périodique.

on fixe la valeur de C puis on augmente  la valeur de L?

on fixe la valeur de L puis  on augmente  la valeur de C?

Qu’observe-t-on ?

Observations et interprétations

Dans les deux cas on observe  que la pseudo-période T d’un circuit (R,L,C) augmente

Donc la pseudo-période T d’un circuit (R,L,C) augmente avec la capacité C et avec l’inductance L.

Equation différentielle la tension aux bornes du condensateur d’un circuit (R,L,C) série

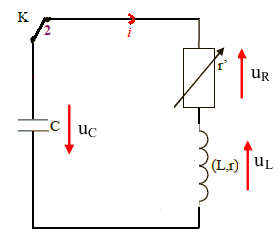
    En appliquant  la loi de la maille

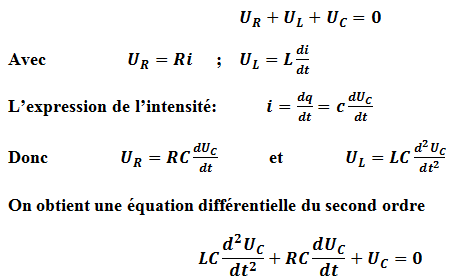
L’équation différentielle du circuit (R,L,C) série vérifiée par U_C(t) la tension aux bornes du condensateur est :

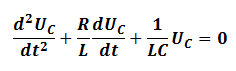
Le terme RLC traduit l’amortissement des oscillations électriques, et sa valeur permet de définir  les différents régimes.

– Pour une inductance L, et une capacité C fixées, on observe trois régimes différents de l’évolution  de U_C(t)  suivant la valeur de la résistance R

Dans le cas du régime pseudo-périodique , la solution de l’équation différentielle s’écrit :

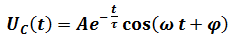
Etude de l’oscillateur non amorti  (L,C)     

             

 On considère un circuit dans lequel on néglige toutes les résistances. Il est constitué d’un condensateur de capacité C et d’une bobine idéale d’inductance L

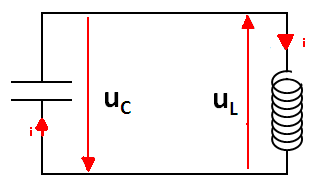
Etablissement de l’équation différentielle

On applique la loi d’additivité des tensions :

Conclusion

Durant les oscillations électriques libres non amorties d’un circuit (L,C)

 la tension aux bornes du condensateur obéit à l’équation différentielle :

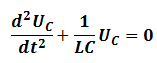
Résolution de l’équation différentielle

Pour l’équation différentielle :

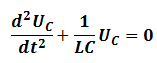
mathématiquement sa solution s’écrit de la forme suivante :

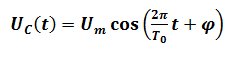
Avec Um, T₀ et φ sont trois constantes à déterminer

• Um : Amplitudes de la tension U_C
• φ : la phase à l’instant t=0  Elle s’exprime en radian   (rad)
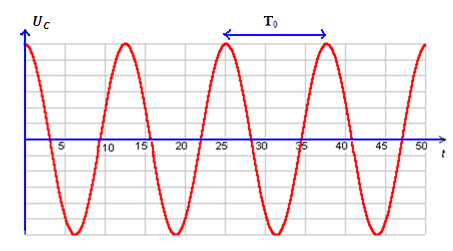
• T₀ : la période propre des oscillations Elle s’exprime en seconde  (s)
• (2π/t0) t+ φ )  : La phase à l’instant (t)

Vérification de la véracité d’une solution

Montrons que la solution proposée est bien solution de l’équation différentielle

Rappel :     derivé d’une fonction composée

                 (cos u_C)’ = – sin u_C x u_C’

(sin u_C)’ =  cos u_C x  u_C’

Conclusion :

La fonction

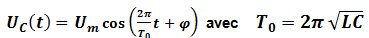
est solution de l’équation différentielle 

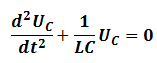
T₀ période propre des oscillations ne dépend que de L et C . son unité dans le système international est le seconde (s) .

Vérification de l’unité de T₀ par analyse dimensionnelle

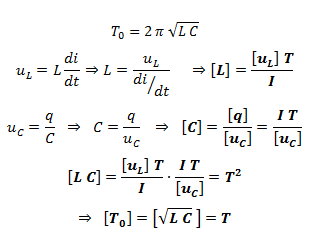
La période propre dont l’expression est :

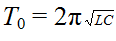
a bien la dimension d’un temps et s’exprime en seconde.

 Détermination des constantes Um et φ

Utilisation des conditions initiales

• à l’instant t = 0, le condensateur est chargé  donc  UC(0) = E

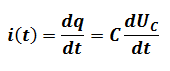
• à l’instant t = 0    

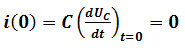
 L’intensité est nulle : i(0) = 0 la bobine n’est traversée par aucun courant électrique.

On étudie donc la « décharge » du condensateur :

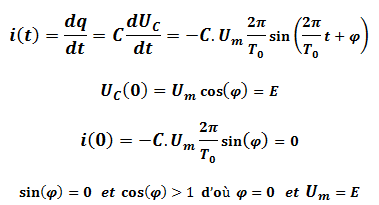
Par conséquent  Expression de la tension aux bornes du condensateur s’écrit :

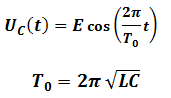
La tension aux bornes du condensateur est une tension alternative sinusoïdale d’amplitude E et de période : T₀   c’est un  régime périodique

Intensité du courant dans le circuit LC

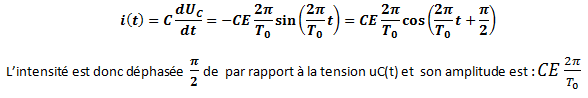
Etude énergétique

Cas d’un circuit LC

Dans un circuit LC, l’énergie totale du circuit   E_T = E_C + E_L

• E_C : l’énergie électrique stockée dans le condensateur
• E_L : l’énergie emmagasinée dans la bobine
• E_T: l’énergie total

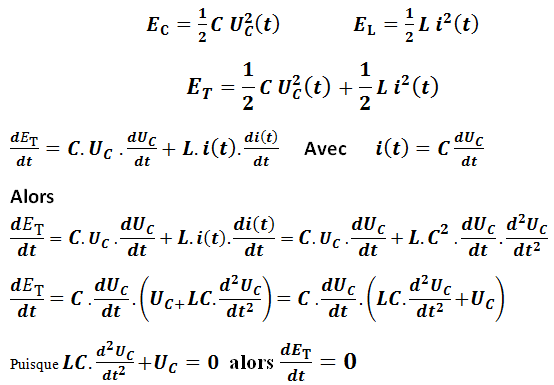
Dans un circuit LC, l’énergie totale du circuit est constante au cours du temps

E_T = E_C + E_L= constante

L’énergie totale se conserve car l’énergie n’est pas dissipée (pas d’effet joule),

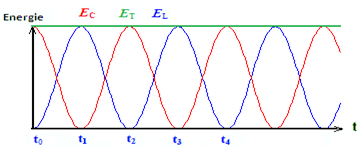
Lorsque l’énergie stocké  dans le condensateur diminue, l’énergie de la bobine augmente et inversement, donc il y a un échange d’énergie entre le condensateur et la bobine au cours d’une  période T₀/2

Temps	Energie EC	Energie EL
t0	EC maximum	0
t1	0	EL maximum
t2	EC maximum	0
t3	0	EL maximum
t4	EC maximum	0

Cas d’un circuit RLC

Dans un circuit RLC, l’énergie totale est E_T = E_C + E_L

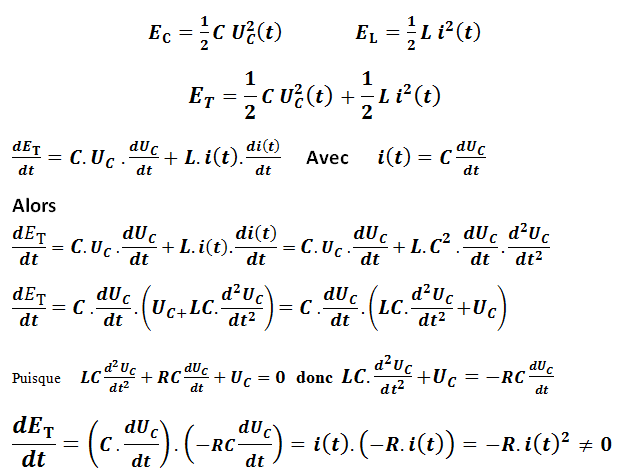
Dans un circuit RLC, au cours de l’échange énergétique entre le condensateur et la bobine, il y a  perte énergétique par effet Joule dans la résistance de puissance R×i²

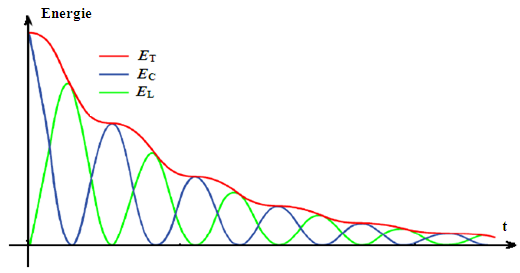
E_T= E_C + E_L ≤  1/2CE²

Entretien des oscillations

Pour le circuit (R,L,C) série, l’amplitude des oscillations décroît à cause  d’une dissipation d’énergie par effet Joule dans le conducteur ohmique.

il est possible d’entretenir les oscillations pour obtenir une amplitude constante des oscillations

Donc Il faut ajouter un dispositif  électronique au le circuit (R,L,C)  pour qu’il devienne équivalent à un circuit LC  .Ce dispositif d’entretien des oscillations possède  une alimentation propre « appelé résistance négative »  possible de fournir au circuit  à chaque instant une énergie équivalente à l’énergie  dissipée par effet joule. L’énergie totale du circuit reste alors constante

 La tension aux bornes de dispositif d’entretien a pour expression U_S(t) = – Ro i(t)

Le dispositif se comporte comme une résistance R₀ négative.

Montage à résistance négative

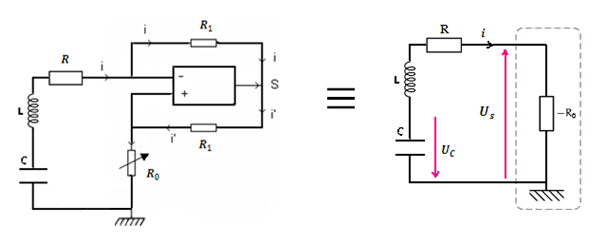
On applique la loi d’additivité des tensions  :

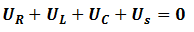
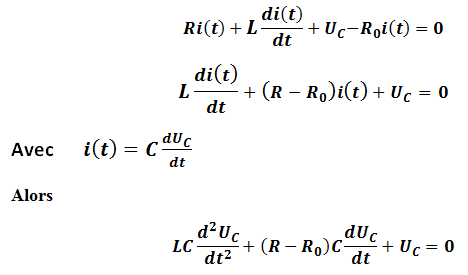
On choisit la résistance réglable R0   égale à R  (résistance  du circuit RLC) donc  l’équation devient :

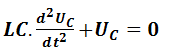
En fin On  aboutit à une équation différentielle semblable à l’équation du circuit LC.

le circuit R LC devient équivalent à un circuit LC et oscille avec une période propre T0 qui dépend seulement à L et C :