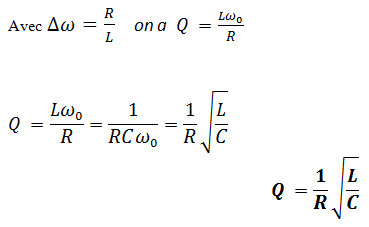cours : circuit RLC série en régime sinusoîdal forcé pour le terminale
Le régime alternatif sinusoïdal
Intensité du courant alternatif sinusoïdal
L’intensité du courant alternatif sinusoïdal s’écrit sous la forme suivante :
i(t) = Im cos (ωt+φi)
Im : l’amplitude maximal , son unité est ampère (A)
ω : la pulsation du courant son unité est rad/s
ωt+φi: la phase du courant à l’instant t . Son unité est rad
φi : La phase à t=0
Intensité efficace du courant :
On note l’intensité efficace d’un courant alternatif sinusoïdal par Ieff et on l’exprime par la relation suivante :
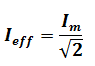
L’ampèremètre utilisé en courant alternatif indique la valeur de l’intensité efficace.
La tension alternative sinusoïdale
La tension alternative sinusoïdale s’écrit sous la forme suivante :
u(t) = Um cos (ωt + φu)
Um : l’amplitude maximal de u(t) unité volt (V)
ω : la pulsation de u(t) , son unité est rad/s
ωt + φu: la phase de u(t) à l’instant t , unité est rad
φu : La phase à t=0
La tension efficace U
La tension efficace Ueff est exprimée par la relation suivante :
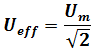
Le voltmètre utilisé en courant alternatif indique la valeur efficace de la tension
Notion de phase
On considère deux grandeurs alternatives sinusoïdales :
i(t) = Im cos (ωt+φi)
u(t) = Um cos (ωt + φu)
Le déphasage ji/u de u(t) par rapport à i(t) est : φu/i = φu– φi
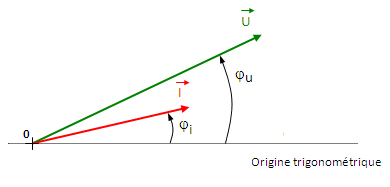
Mesure du déphasage entre deux signaux sinusoïdaux à l’aide d’un oscilloscope.
Le décalage horaire
Définition :
Le décalage horaire τ est l’intervalle de temps qui sépare deux maximums successifs ou 2 annulations successives des 2 fonctions sinusoïdales quand elles varient dans le même sens.
L’expression du déphasage à partir des mesures de la période T et du décalage τ est
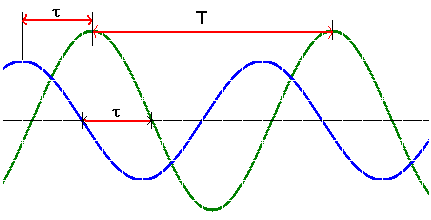
φu/i= 2 π (τ / T) j s’exprime en radians
Identification du signal en avance ou en retard :
Le signal qui est en avance de phase par rapport à l’autre est celui qui s’annule avant l’autre lorsque les deux signaux sont dans le même sens.
φu/i mesure l’avance et la retard de chaque fonction par rapport à l’autre.
φu/i > 0 : u(t) est en avance sur i(t)
φu/i < 0 : u(t) est en retard sur i(t)
φu/i = π/2 : u(t) et i(t) sont en quadrature de phase
φu/i = π : u(t) et i(t) sont en en opposition phase
φu/i = 0 : u(t) et i(t) sont en phase .
Étude expérimentale du circuit (R,L,C) série en Régime alternatif sinusoïdal
Activité 1
Visualisation de la tension u(t) aux bornes d’un circuit (R,L,C) et i(t) en fonction du tempsو
On alimente le circuit RLC série avec un générateur de basse fréquence (G.B.F) délivrant une tension sinusoïdale u(t)=Um sin(wt+ju).
On fixe la fréquence sur N = 100Hz et Um = 2V
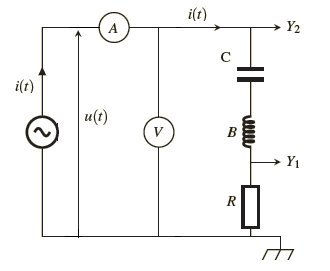
A l’aide d’un oscilloscope :
la tension uR(t) sera visualisée sur la voie Y1
la tension u(t) sera visualisée sur la voie Y2,
A l’aide d’un ampèremètre :
On mesure l’intensité efficace I du courant qui traverse le circuit
A l’aide d’un voltmètre
On mesure la tension efficace U aux bornes du circuit (R,L,C) .
On obtient les oscillogrammes suivants
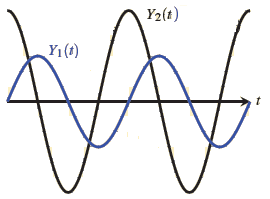
Exploitation des résultats
Sur la voie Y1 il apparaît une fonction sinusoïdale qui représente la tension aux bornes de la résistance R uR(t).
La visualisation de la tension uR(t) nous permet de visualiser l’intensité instantanée i(t)
D’après la loi d’Ohm , on a uR(t) = Ri(t) la tension est inversement proportionnel à i(t)
Donc Il apparaît dans le circuit un courant électrique d’intensité : i(t) = Im cos (ωt )
En faisant varier la fréquence du G.B.F, on remarque, en utilisant les oscillogrammes, que les deux tensions u(t) et uR(t) ont la même période (même fréquence) ,
La fréquence des oscillations de la tension uR(t) est imposée par le générateur,: on dit que les oscillations sont forcées.
Le générateur joue le rôle de l’excitateur.
Le dipôle RLC en série joue le rôle du résonateur.
Impédance circuit R-L-C série.
Activité 2
On fixe la fréquence f1 = 100 Hzde la tensionimposée par le GBF et on fait varier sa valeur efficace Ueff.. On mesure alors l’intensité efficace Ieff qui parcourt le circuit.
On recommence l’expérience pour une fréquence f2 = 500 Hz.
on les regroupe les valeurs prise dans le tableau suivant :
| Ueff (V) | 5 | 10 | 15 | 20 | |
| f1=100 Hz | Ieff (A) | 0,07 | 0,13 | 0,20 | 0,27 |
| f2=500 Hz | Ieff (A) | 0,07 | 0,13 | 0,20 | 0,27 |
On trace la courbe
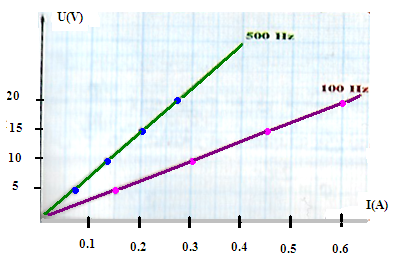
On remarque que, pour chacune des fréquences choisies, Ueff est inversement proportionnelle à Ieff.. avec Z un facteur de proportionnalité.
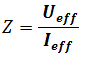
Ueff tension efficace mesurée par le voltmètre.
Ieff. intensité efficace mesurée par l’ampèremètre.
Z est appelé : l’impédance du circuit RLC série son unité dans le système internationale est Ω.
Influence de la fréquence
Lorsqu’on fait varier la fréquence du circuit (R,L,C) on observe que l’impédance Z change, donc l’impédance Z dépend de la fréquence du circuit.
Etude théorique du circuit (R,L,C)
But :
Déterminer l’Impédance du circuit RCL en série
Déterminer l’angle de déphasage du circuit RCL en série
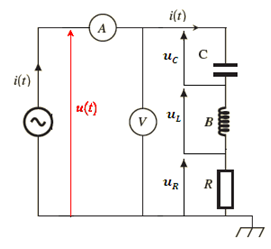
Un circuit (R,L,C) en série alimenté sous une tension alternative sinusoïdale est traversés par le même courant alternatif sinusoïdal. Autrement dit, le courant qui traverse la résistance, l’inductance et la capacité branché en série est le même et identique courant.
i(t) = Im cos (ωt)
u(t) = Um cos (ωt + φ)
φ :phase de u(t) par rapport à i(t)
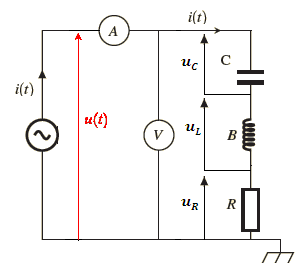
A l’aide de vecteur de Fresnel on facilite les calculs.
I°/ Le vecteur de Fresnel associé à une grandeur sinusoïdale :
On associe à une fonction sinusoïdale du temps y = a cos (ωt + φ) un vecteur appelé vecteur de Fresnel :

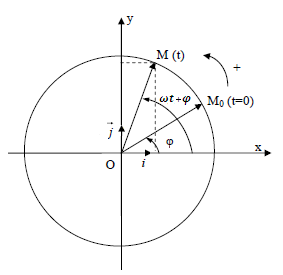
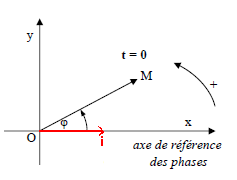
La tension aux bornes de la résistance
Un courant i(t) va traverser la résistance et pour chaque instant t on a :
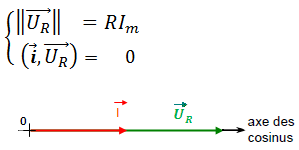
uR(t) =Ri(t) =RIm cos (ωt)
Le courant et la tension sont en phase ∆φ = 0
Représentation de Fresnel correspondante :
La tension aux bornes de la bobine
Un courant va traverser l’inductance et pour chaque instant t on a :

Représentation de Fresnel correspondante :
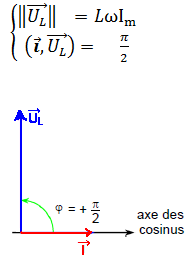
La tension aux bornes de condensateur
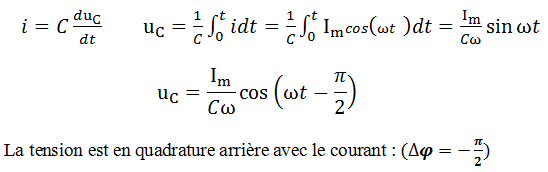
Représentation de Fresnel correspondante :
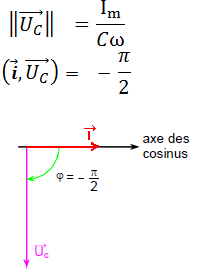
uR, uL, uC déjà calculer donc d’après La loi d’addition des tensions :
u(t)= uR+ uL+ uC
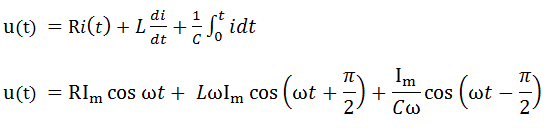
Mathématiquement la somme de cette équation est à la forme :
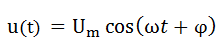
On utilise la méthode de Vecteurs de Fresnel pour simplifier l’équation
u(t)= uR+ uL+ uCen valeurs instantanées
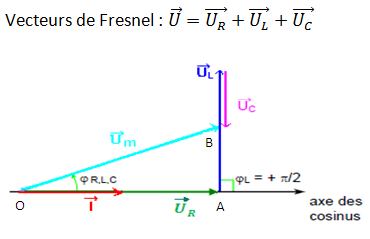
On a un triangle rectangle en A donc appliquons le théorème de Pythagore on écrit :
OA2 + AB2 =OB2
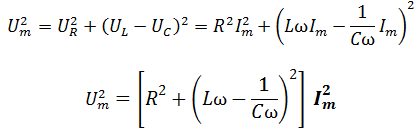
Détermination l’Impédance du circuit RCL en série
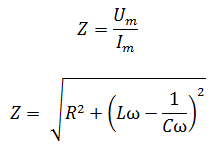
On constate que l’impédance Z est en fonction de la pulsation ω
Détermination l’angle de déphasage
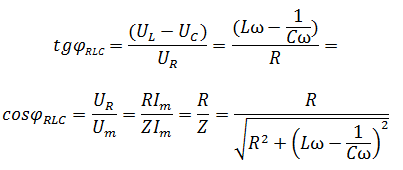
On constate que l’angle de déphasage est en fonction de la pulsation ω
Phénomène de résonance d’intensité
Activité 3
On réalise le montage électrique où le générateur à basse fréquence alimente le circuit (R,L,C) série d’une tension alternative sinusoïdale de valeur efficace U et de fréquence f réglables .
– Une bobine d’inductance L=5,2mH et de résistance r = 7Ω.
– Un condensateur de capacité C = 0,47F.
Fixer la tension efficace sur la valeur U=4V et la résistance globale R = r+r’ sur la valeur R1 = 37Ω.
Faire varier la fréquence f du générateur en mesurant l’intensité efficace I du courant.
Régler la résistance globale R sur la valeur R2 = 107Ω en faisant varier la résistance r′ du conducteur ohmique et répéter l’étape précédent de l’expérience.
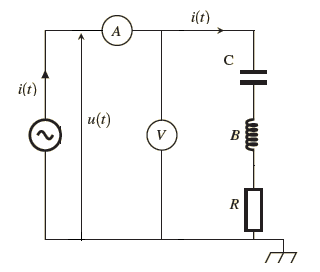
On regroupe les résultats dans le tableau suivant :

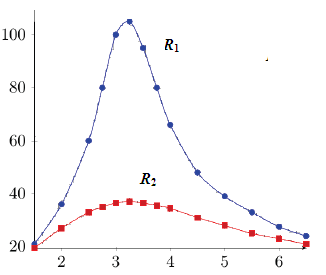
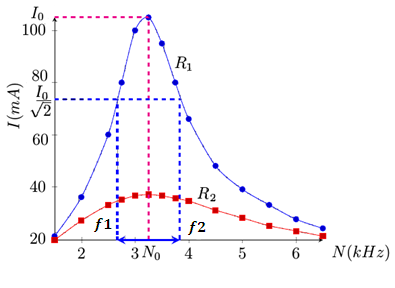
1. Représenter dans le même repère les deux courbes I en fonction de f pour les deux résistances R1 et R2 du circuit
Exploitation des résultats
Définition
Le circuit est à la résonance d’intensité lorsque l’intensité efficace est au maximum.
Le phénomène de résonance apparaît, lorsque la fréquence de résonance imposé par le générateur devient égale à la fréquence propre du circuit (R,L,C)
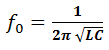
Questions
D’après la courbe déterminer la fréquence de résonance f et Intensité I0.
Calculer la fréquence propre f0 du résonateur du circuit l’oscillateur RLC.
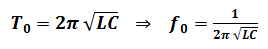
Comparer entre les 2 valeurs f et f0.
Calculer Z l’impédance du circuit à la résonance et la comparer avec la résistance globale R du circuit dans les deux cas.
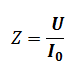
La résonance correspond à un maximum d’intensité, donc à une impédance minimale
Observation et Interprétation
Lorsque la fréquence du générateur « excitateur » varie, l’intensité dans le circuit (R,L,C) « résonateur » varie : elle augmente peu à peu, passe par un maximum pour une fréquence « appelée fréquence de résonance », puis diminue à nouveau.
D’après la courbe I=f(N)
On détermine de la fréquence de résonance
La fréquence de résonance f = 3250Hz est le même pour deux résistances
R1 =37Ω et R2 = 107Ω
L’intensité efficace maximale à la résonance pour R1 = 37Ω est I0= 105 mA
L’intensité efficace maximale à la résonance pour R2 = 107Ω est I0= 37 mA
Le calcul de la fréquence propre f0 du circuit
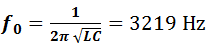
On remarque f0 ≈ f
Le phénomène de résonance apparaît, lorsque la fréquence du générateur « excitateur » s’identifie à la fréquence propre du circuit (R,L,C).
On détermine l’impédance du circuit à la résonance
L’impédance du circuit à la résonance : pour la courbe R1
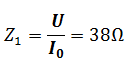
L’impédance du circuit à la résonance : pour la courbe R2
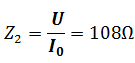
le calcul de l’impédance du circuit est à peu près égale à la résistance globale du circuit
À la résonance, l’impédance du circuit (R,L,C) est égale à la résistance globale du circuit le circuit (R,L,C) se comporte comme un inducteur ohmique de résistance Z= RT.
Le rôle de la résistance globale du circuit.
Tant que la résistance R du circuit est petite , l’intensité efficace maximale du courant à la résonance est grande et la résonance est aiguë . (amortissement du circuit est faible)
Si R est grande l’intensité efficace maximale du courant est petite et la résonance est floue .
(l’amortissement du circuit est fort),
On détermine La phase φ à la résonance
À l’aide d’un oscilloscope, on observe qu’à la résonance i(t) et u(t) sont en phase φu/i = 0.
Bande passante
La bande passante à – 3 dB d’un circuit (R, L, C) série correspond à l’intervalle des fréquences [f1; f2] du générateur, pour lesquelles le circuit donne une réponse (en intensité) importante pour laquelle l’intensité efficace I du courant vérifie la relation suivante:
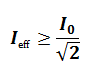
I0 : intensité efficace à la résonance
Détermination de la bande passante
Pour la résistance R1 = 37Ω I0= 105 mA

Pour R2 = 107Ω est I0= 37 mA
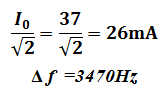
Si R est petite la bande passante Δ f est petite la résonance est aiguë
Si R est grande la bande passante Δ f est grande la résonance est floue
Facteur de qualité
Le facteur de qualité Q correspond à :
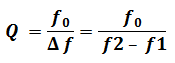
Détermination de facteur de qualité Q
Pour la résistance R1 = 37Ω I0= 105 mA
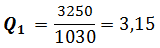
Pour R2 = 107Ω est I0= 37 mA
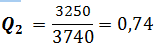
Remarque
Le circuit est d’autant plus sélectif que Q est sera grand.
Autant que la résonance est aiguë plus la valeur de Q est grande.
Etude théorique
Détermination de la fréquence à la résonance

Détermination d’impédance du circuit à la résonance
à la résonance l’Impédance du circuit (R,L,C) est minimal
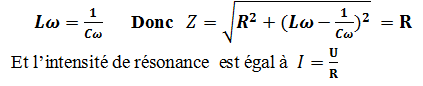
Détermination la phase φ à la résonance.
vu précédemment que
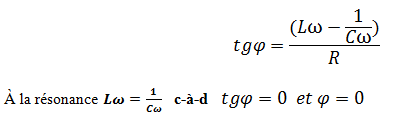
à la résonance les deux tensions u(t) et uR(t), sont en phase alors i(t) et u(t) sont en phase
Détermination de la bande passante
On considère la fonction I= f(ω) représenté par la courbe suivante
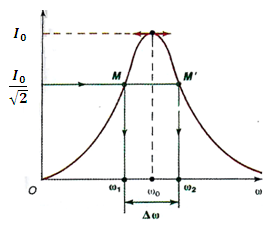
On raisonne ici avec les pulsations ω=2πf
Cherchons ω1 et ω2 pour délimiter la bande passante c.à.d. [ω1, ω2]
La largeur de la bande passante est : Δw = ω2 – ω1
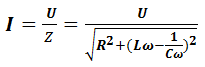
à la résonance l’intensité est maximal et impédance est minimal égal à la résistance ohmique.
Alors
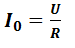
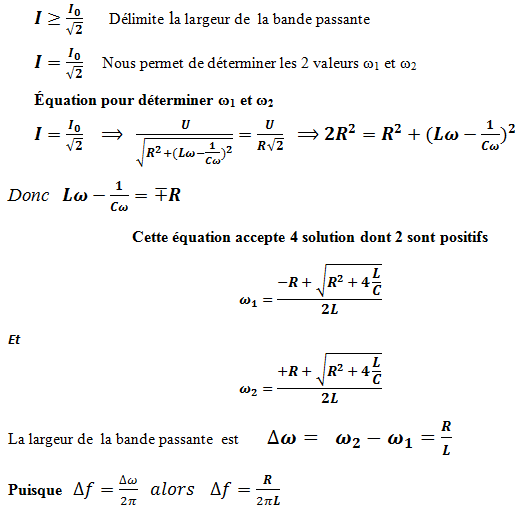
Dans le cas où R est petite le circuit très peu résistif et la bande passante est étroite. On dit que le circuit est très sélectif .
Détermination de Facteur de qualité
Le facteur de qualité Q correspond à :
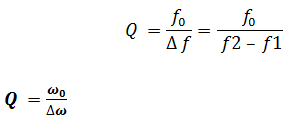
w0 la pulsation propre du circuit (R,L,C) Δw La largeur de la bande passante