Référentiel et repère
Un référentiel est un objet par rapport auquel on étudie un mouvement. C’est dans ce référentiel que sera définit le repère d’espace utilisé pour suivre le mouvement Le plus souvent, dans notre étude c’est le repère cartésien et orthonormé.
Les principaux référentiels:
Le référentiel terrestre : le solide de référence est un objet fixe à la surface de la Terre. (un point du sol et de trois axes, un axe vertical et deux axes dans le plan horizontal ). Ce référentiel est adapté à l’étude du mouvement d’un objet proche de la surface de la Terre.
Le référentiel géocentrique : le solide de référence est le centre de la Terre les trois axes pointant vers des étoiles fixes suffisamment lointaines Ce référentiel est adapté à l’étude du mouvement des satellites en orbite autour de la Terre.
Le référentiel héliocentrique : le solide de référence est le centre du Soleil. les trois axes pointant vers des étoiles fixes suffisamment lointaines Il est adapté à l’étude des mouvement du système solaire ( comme celui des planètes
Les grandeurs de l’évolution
1- Le vecteur de position
Pour l’ étude du mouvement d’un corps nous étudions uniquement le mouvement du centre d’inertie G, parce qu’il nous permet de connaître le mouvement global du corps.
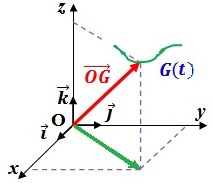
On repère le point mobile G d’un corps solide, dans un repère orthonormé R (𝑶, 𝒊⃗, 𝒋⃗, 𝒌⃗) lié au corps référentiel, à chaque instant, par le vecteur position :
undefined undefined
𝒙 et 𝒚 et 𝒛 sont les coordonnées cartésiennes du point mobile G dans le repère R .
2-Le vecteur vitesse
On définit le vecteur vitesse V comme la dérivée du vecteur de position en fonction du temps.
Le vecteur vitesse moyenne :
Pendant le déplacement d’un mobile du point G , vers le point G’, entre deux instants t et t’ par rapport à un référentiel donné, son vecteur vitesse moyenne entre ces deux instants est:
undefined

Le vecteur vitesse instantanée :
On détermine le vecteur vitesse instantanée du centre d’inertie G ’un corps solide mobile à l’instant ti en déterminant le vecteur vitesse moyenne du point G entre deux instants ti-1 et ti+1 très proches, Cette méthode est appelée méthode d’encadrement ( l’instant ti est encadré par deux instants ti+1 et ti-1 très proches).
undefined
Pour obtenir la vitesse instantanée il faut que Δt→𝟎 alors, On montre mathématiquement que :
undefined undefined
Dans un référentiel donné, le vecteur vitesse instantanée du centre d’inertie G d’un corps solide est égal la dérivée par rapport au temps du vecteur position :
undefined
Le vecteur vitesse instantanée dans un repère cartésien :
undefined
Soient 𝐕𝒙 et 𝐕𝒚 et 𝐕𝒛 les coordonnées cartésiennes du vecteur vitesse
undefined
3-Le vecteur accélération :
on définit le vecteur-accélération 𝒂⃗G en utilisant la relation d’encadrement approchée ( l’instant ti est encadré par deux instants ti+1 et ti-1 très proches).
undefined
Mathématiquement, on exprime le vecteur accélération par la relation
undefined
Enfin on définit que dans un référentiel donné, le vecteur accélération du centre d’inertie G d’un corps solide à l’instant t est égal la dérivée par rapport au temps du vecteur vitesse au même instant :
undefined undefined
Le vecteur accélération dans un repère cartésien :
undefined undefined
𝒂𝒙 et 𝒂𝒚 et 𝒂𝒛 sont les coordonnées cartésiennes du vecteur accélération 𝒂⃗𝑮 .
undefined
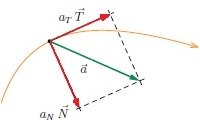
Le vecteur accélération dans la base de Frenet
La base de Frenet (G , 𝒖⃗ , 𝒏⃗ )est un repère a pour origine le centre de gravité du mobile; et ses vecteurs unitaires sont :
- 𝒖⃗ : vecteur orienté selon la tangente à la trajectoire et orienté dans le même sens que le mouvement .
- 𝒏⃗ : vecteur orienté normal à la trajectoire (perpendiculaire à𝒖⃗ ) et orienté vers l’intérieure de la concavité de la trajectoire.
on exprime le vecteur accélération 𝒂⃗G dans le repère de Frenet, pour un mouvement curviligne comme suit : 𝒂⃗G = 𝒂⃗T+𝒂⃗N
- 𝒂⃗T=aT.𝒖⃗ est le vecteur accélération tangentielle aT=𝒅𝑽/𝒅𝒕
- 𝒂⃗N=aN.𝒏⃗ est le vecteur accélération normale aN=VG2/ρ avec 𝝆 le rayon de courbure de la trajectoire à la positionG .
Première loi de Newton ou principe d’inertie
Dans un référentiel Galiléen , si la somme vectorielle des forces extérieures appliquées à un corps solide est nulle
undefined
alors le vecteur vitesse 𝑽⃗𝑮 de son centre inertie G du solide reste constant:c-à-d que G est au repos ou en mouvement rectiligne uniforme . Réciproquement , si le vecteur vitesse 𝑽⃗𝑮 de centre d’inertie d’un solide reste constant , la somme des forces qui s’exercent sur le solide est nulle
undefined
Remarque : le repère Galiléen est un repère dans lequel le principe d’inertie est vérifié
La deuxième loi de Newton:
La force extérieure appliquée à un corps solide est un agent du changement pour le mouvement. C’est-à-dire elle modifie le vecteur vitesse v (module et /ou direction de vecteur). Donc dans un référentiel Galiléen, la somme vectorielle des forces extérieures appliquées à un corps solide est égale au produit de sa masse 𝒎 et du vecteur accélération 𝒂⃗G
undefined
Troisième loi de Newton
Énoncé de la loi : le principe d’interaction mutuelles
Lorsqu’on a deux corps A et B en interaction, ils exercent l’un sur l’autre des forces qui sont égales et opposées entre elles
undefined
Quelque soit l’état des deux corps : soient en mouvement ou en repos.