Le Champ de pesanteur
Tout corps de masse m situé au voisinage de la terre est soumis à une force de d’attraction gravitationnelle qui peut s’identifier à la force de pesanteur P . La Terre crée un champ de pesanteur 𝐠⃗. Tout corps de masse 𝑚 placé dans le champ de pesanteur 𝐠⃗ subit une force de pesanteur appelé poids possédant : La valeur de l’intensité g de la pesanteur dépend de la latitude (g = 9,78 N / kg à l’équateur, g = 9,83 N / kg au pôle Nord, au niveau de la mer)
- une origine : centre d’inertie G du corps
- une direction : la verticale passant par G
- un sens : du haut vers le bas (centre de la Terre)
- une valeur : P = m g
Unités :
- P : poids en newton (N)
- m : masse en kg
- g : intensité de la pesanteur en (N / kg) ou en (m / s²)
Poussée d’Archimède (Force exercée par le fluide)
Tout corps immergé dans un fluide que soit immobile ou en mouvement est soumis de la part de celui-ci à un ensemble de forces de pression équivalentes à une force unique , appelée poussée d’Archimède :FA
- de direction verticale ;
- orientée vers le haut ;
- de valeur égale au poids du fluide déplacé.
- 𝛒𝐟luide :masse volumique du fluide kg.m-3
- 𝑉 :volume du fluide déplacé (égal au volume du corps immergé ) m3
- 𝑔: valeur du champ du pesanteur
Force de frottement exercé par le fluide.
Lorsqu’un solide est en mouvement dans un milieu fluide, il subit de la part de ce fluide un ensemble de forces de frottement équivalentes à une force unique F= k vn , appelée force de frottement fluide s’opposant au mouvement du solide.
- origine : le centre d’inertie G
- direction : la verticale
- sens : opposé au mouvement
– intensité : F = kvn où k est une constante qui dépend de la forme de l’objet et de la nature du fluide, et n un nombre, entier ou non, qui dépend entre autre de la vitesse de l’objet.
- Pour des vitesses faibles, et des objets de petites dimensions, n = 1.
- Pour des vitesses élevées, et des objets de dimensions plus importantes, n = 2 .
- Dans les deux cas le coefficient k dépend de la nature du fluide et de l’objet
Etude expérimentale de la chute d’une bille dans un liquide
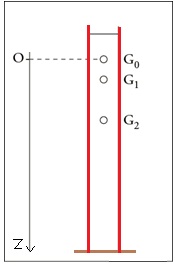
Une petite bille d’acier de masse m de rayon r est lâchée, sans vitesse initiale, dans un mélange d’eau et de glycérol de masse volumique 𝛒𝐟luide à partir de l’origine d’un axe vertical (O, 𝒌⃗ ) orienté vers le bas.
Etudions la bille en chute verticale sur l’axe Oz dans le référentiel terrestre considéré comme galiléen
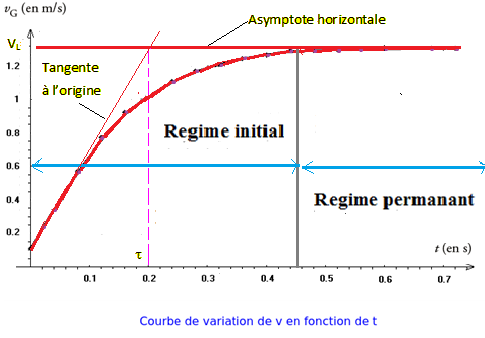
On enregistre le mouvement de la bille dans le liquide à l’aide d’un camera numérique On obtient la courbe vG= f (t) suivant :
La position instantanée du centre G de la bille est repérée sur l’axe vertical orienté vers le bas OZ, par l’intermédiaire d’un webcam couplée à un ordinateur « acquisition vidéo déclenchée de manière à enregistrer une vingtaine d’ images par seconde »L’ analyse est fait à l’aide d’un logiciel permettant de repérer aux dates t i les positions successives x i de G lors de son mouvement descendant et de calculer approximativement la vitesse moyenne v i entre les dates t i -1 et t i + 1.
A partir du graphe , on décrit le mouvement de chute et on mesure la vitesse limite vlim :
- Régime initial : sur l’intervalle [0 ; 0,44 s] la vitesse augmente
- Régime permanent : à t >0,44 s La vitesse se stabilise et reste constante avec une vitesse limite vlim= 1,23
L’accélération du bille aG: (à partir du graphe)
Le vecteur accélération aG =dvG/dt vertical sur l’axe Oz
- à t=0 la valeur d’accélération a0 est le coefficient directeur de la tangente à la courbe à l’instant à t=0 a0 =ΔvG/Δt= 6,12m/s
- à t >0,44 s vlim est constant donc la valeur d’accélération est nul aG=0
En régime initial : la valeur d’accélération diminue au cours de temps
En régime permanent : aG = 0 donc le mouvement de la bille est vertical uniforme
Interprétation qualitative des variations temporelles
Au départ t=0 « état initial » Une fois la bille est à la surface à une vitesse nulle il est soumis à deux force :« la force de frottement fluide est nulle »
- Poids du corps solide 😛
- Poussé d’Archimède :FA
En projetant la relation vectorielle obtenue sur l’axe Oz :La somme des forces est égal à:
en général la poussée d’Archimède est plus petite que celle du poids
donc la bille se met en mouvement à t=0 avec une accélération initial a0 , la vitesse commence à augmenter ce qui entraine l’augmentation de la valeur de la force de frottement fluide . La somme des forces extérieures diminue progressivement de même de la valeur du vecteur d’accélération et tend au bout d’un certain temps vers une vitesse limite vlim « le vecteur accélération est alors nul »
Étude théorique :
- Référentiel utilisé
On considère le Référentiel : terrestre supposé galiléen comme repère d’étude du mouvement du centre d’inertie G de la bille.
- Force extérieures
Bilan des force extérieures qui agissent sur la bille au cours de mouvement .
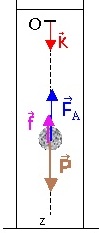
Appliquons la deuxième loi de Newton au mouvement de G de la bille :
En projetant la relation vectorielle obtenue sur l’axe Oz :
on a: m=ρbille .V
Au départ t=0 « état initial » une fois la bille est à la surface à une vitesse nulle « force de frottement est nulle » f=0 donc:
Lien entre τ, a0 et vlim :
La tangente à l’origine coupe l’asymptôte de la courbe vG(t) au point d’abscisse t = τ et on a la relation : vlim = a0 × τ
τ: appelé temps caractéristique du mouvement.







