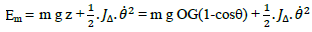Étude énergétique du pendule élastique horizontal

Travail de la force exercée sur l’extrémité d’un ressort

Rappel

Travail d’une force constante

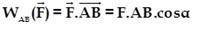
On exprime le travail d’une force constante lors du déplacement quelconque du point d’application de A vers B par la relation:

F exprimée en newton (N) et le travail W  exprimé en joule (J) .

Le travail d’une force constante ne dépend pas de la trajectoire suivie par son point d’application , il ne dépend que de la position initiale et finale .

Travail d’une force variable et d’un déplacement non rectiligne

 Lors du déplacement  de A vers B où la force change  et le trajet n’est pas rectiligne, on  divise le trajet en petits éléments rectilignes parcourus durant un  temps Δt—-0   sur lesquels on considère que la force F reste pratiquement constante.

Le travail élémentaire effectué par la force est:

Le travail effectué par la force entre les points A et B est égal à la somme des travaux  élémentaires :

Pour calculer la somme d’une façon plus précise on remplace le symbole somme  par le symbole intégrale

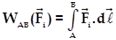
Travail de la force de rappel du ressort d’un pendule élastique horizontal

On sait que la force de rappel du ressort s’écrit:

 Durant le déplacement infinitésimal la force reste pratiquement constante alors   Le travail infinitésimal que la force effectue  lors d’allongement dl  du ressort  s’écrit :

dW = .=-K x. dx=-K x dx

Le travail que la force F effectue pour que l’allongement de ressort passe de  la position A  d’abscisse  x_A  à la position B d’abscisse x_B est :

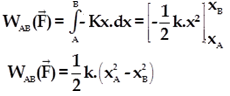
Unités : W est en joule (J) – K en newton par mètre (N / m) – X en mètre (m)

On constate que le travail de cette force ne dépend pas du chemin suivi, il est « conservative ».

 Énergie potentielle élastique du système horizontale

Un ressort de de raideur k possède de l’énergie potentielle élastique  notée E_Pe , lorsqu’il est allongé ou comprimé  d’ une élongation x,   son expression est:

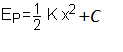
Unité: Ep (J), k (N.m^-1), x(m).

Par convention on choisit Ep = 0 pour x = 0 donc  C = 0 et

• x = Δl est l’allongement du ressort en mètre
• C : La constante dépend  du choix de l’état de référence  de l’énergie potentielle.

La variation d’énergie potentielle élastique d’un ressort est l’énergie transférée durant son allongement de x_A à x_B s’écrit:

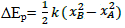
Le travail de la force de rappel calculé déjà est:

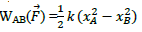
D’où:

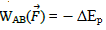
Énergie cinétique 

L’énergie cinétique E_C  du pendule élastique est celle du solide(S) en translation, puisque la masse du ressort est négligeable, l’expression de E_C en fonction du temps s’écrit:  

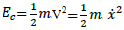
     Unité E_C : joule (J)

Énergie mécanique du système horizontale

L’énergie mécanique du système {solide, ressort} dans le plan horizontal est la somme d’énergie potentielle et d’énergie cinétique :  E_m = E_c + E_p

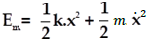
l’état de référence est pris (Ep = 0)

Conservation de l’énergie mécanique

Cas de frottement négligeable

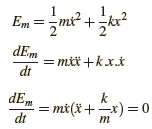
Nous avons vu que l’équation différentielle du mouvement est : donc E_m est constante ,l’énergie mécanique se conserve.

Calculons l’énergie mécanique d’un ressort élastique en mouvement de translation.

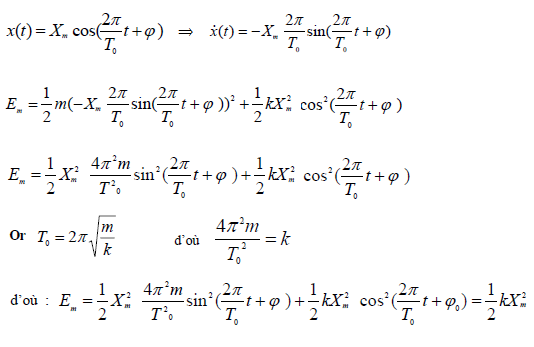
l’énergie mécanique du système horizontal est constante  en l’absence de frottement,: E_m=cte

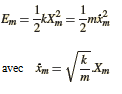
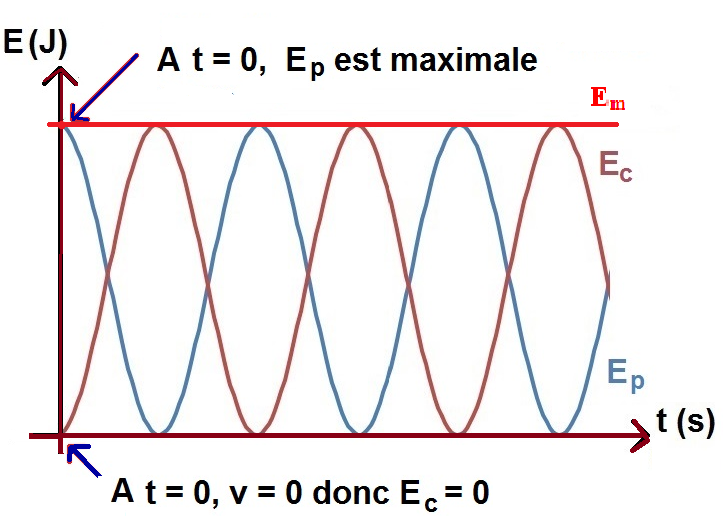
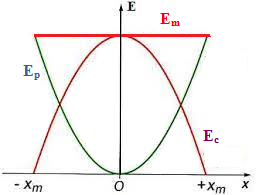
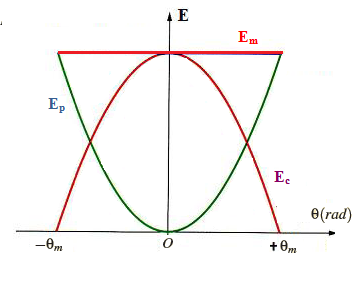
A l’instant t=0,  début d’élongation initiale du ressort l’énergie potentielle E_p  est maximum egal à  E_m  alors que  l’énergie cinétique E_c est nulle. Puis, E_p  commence à diminuer  en  se rapprochant de la  position d’équilibre,  en même temps E_c augmente. l’objet passe par la position d’équilibre, E_p = 0  et  E_c est maximum egal à E_m. L’objet commence à se ralentir quand  il  dépasse la position d’équilibre donc Ec diminue.et Ep augmente.

on peut résumer cette rédaction par des courbes:

Étude énergétique d’un pendule de torsion

 Travail du couple de torsion

Le moment du couple de torsion  est : M_c = – C 𝜃̇

le travail élémentaire dW_c du  moment  du couple torsion M_c  lors d’un déplacement élémentaire d𝜃̇ est :

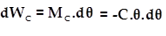
Le travail effectué lors du déplacement  de la position A d’abscisse angulaire 𝜃̇_A vers une position B d’abscisse angulaire 𝜃̇_B  est égal à la somme des travaux élémentaires :

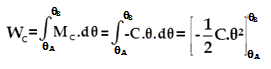
d’où la valeur du travail:

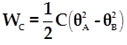
On constate que le travail de ce couple de torsion ne dépend pas du chemin suivi

On peut calculer le travail du couple de torsion en appliquant le théorème d’énergie cinétique au système oscillant entre deux positions 𝜃̇₁ et 𝜃̇₂

Énergie cinétique

On définit l’énergie cinétique du système qu’est en rotation autour de Δ, par l’expression suivante

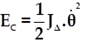
• J_Δ: le moment d’inertie de la tige par rapport à l’axe de rotation matérialisé par le fil métallique
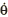• : la vitesse angulaire de la tige à instant t .

Puisque : donc

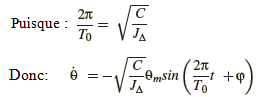
D’où l’expression de E_C:

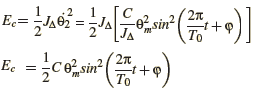
calculons le travail du couple de torsion en appliquant le théorème d’énergie cinétique entre deux positions 𝜃̇₁ et 𝜃̇₂

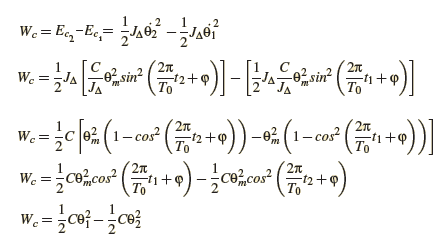
Cette expression montre que le travail du couple de torsion entre ces deux position est égale à la la variation de l’énergie potentielle de torsion

Énergie potentielle de torsion

Un fil de torsion tordu possède une énergie potentielle de torsion E_P d’expression:.

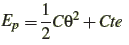
Cte : constante dépend de l’état de référence de l’énergie potentielle de torsion

Énergie mécanique du système oscillant

L’énergie mécanique d’un pendule de torsion est défini par la relation suivante :

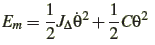
Conservation de l’énergie mécanique

On dérive l’expression  de E_m par rapport au temps  :

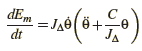
En cas de frottement négligeable, le pendule de torsion est  libre non amorti donc son équation différentielle s’écrit:

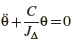
Par conséquent: donc E_m est constant cela montre que l’énergie mécanique d’un pendule de torsion libre et amorti se conserve

Diagramme d’énergie d’un pendule de torsion :

Lorsque la tige passe par sa position d’équilibre : E_p=0 ,

Dans la position 𝜃̇=𝜃_m 𝐸𝑐=0 , ,

Étude énergétique d’un pendule pesant

Énergie cinétique d’un pendule pesant

Le mouvement du pendule pesant est un mouvement de rotation oscillatoire, son énergie cinétique a pour expression:

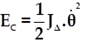
•  J_Δ : moment d’inertie du pendule par rapport à l’axe Δ  exprimé en kg.m²
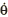• : vitesse angulaire du pendule en rad/s
• E_c: énergie cinétique en joule (J) .

L’énergie potentielle de pesanteur d’un pendule pesant est donnée par l’expression suivante :

E_pp = mg z+C

• m : la masse du pendule en (kg),
• g: intensité de pesanteur en (ms^-2 ),
• z : l’altitude du centre d’inertie G du système sur l’axe (O,z) d’un repère orthonormé orienté vers le haut
• C: dépend de l’état de référence pris pour E_PP , l’énergie potentielle est nulle (E_pp,réf= 0 )

 

Énergie potentielle de pesanteur

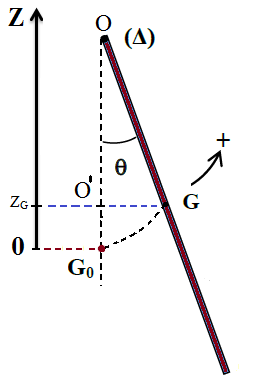
Z_G indique la position du centre d’inertie du pendule pesant

Z_G =O’G₀=OG₀ – OO’=OG – OO’   avec   OO’=OG.cos(𝜃̇)
Z_G=OG – OG.cos(𝜃̇)=OG (1- cos(𝜃̇) )

Si on prend la position d’équilibre (𝜃̇=0) comme état de référence C=0,

E_pp = mg OG[1- cos(𝜃̇) ]

Pour des faibles oscillations (θ ⩽ 15°) on peut écrire l’approximation 1-cosθ ≃ 𝜃/2

alors l’expression de l’énergie potentielle de pesanteur s’écrit donc

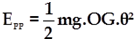
Énergie mécanique

L’expression de l’énergie mécanique du pendule pesant :

E_m = E_pp + E_c