Cours complet: le dipôle RL pour le terminale ( Bac Français )

La bobine

1. Définition

Une bobine est constituée  par un enroulement cylindrique d’un fil de conducteur, enroulé un grand nombre de spire  recouvert d’une couche isolante (gaine ou vernie) .

Représentation symbolique :

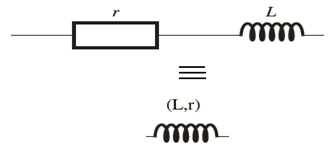
L : inductance, exprimée en henry (H),

r : résistance interne, exprimée en ohm (Ω)

L’inductance L d’une bobine   est mesuré par un appareil de mesure appelé « l’inductance».

Influence d’une bobine dans un circuit

1) Retard à l’établissement du courant

Activité 1

On réalise le circuit suivant où les deux lampes L1 et L2 sont identiques.

 On ferme l’interrupteur K

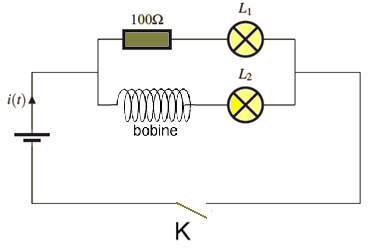
Observez les deux lampes de chaque branche lors de la fermeture de l’interrupteur K. Que remarquez-vous ?

0bservation et interprétation

 La lampe L₁ s’allume instantanément après la fermeture de l’interrupteur, alors qu’il faut quelques instants pour que la lampe L₂ s’allume normalement, avec le même éclat que L₁

On remarque que la lampe située dans la branche comprenant la bobine s’allume en retard par rapport à celle de l’autre branche.

Conclusion :

Dans un circuit électrique la présence d’une bobine retarde l’établissement du courant dans ce circuit

2) Surtension à l’ouverture du circuit:

A l’ouverture  de l’interrupteur, on voit une étincelle apparaître entre les contacts. Sans  bobine dans le  circuit, l’étincelle n’apparaît plus.

Il apparaît une surtension aux bornes de la bobine ce qui entraine  la formation d’une étincelle de rupture au niveau des contacts de l’interrupteur.

Comportement d’une bobine

Relation entre l’intensité du courant électrique et la tension aux bornes d’une bobine

Activité 2  On constitue un circuit série, formé d’un générateur de tension en « dents de scie » « G.B.F ». d’une bobine de résistance interne faible, d’une résistance R.

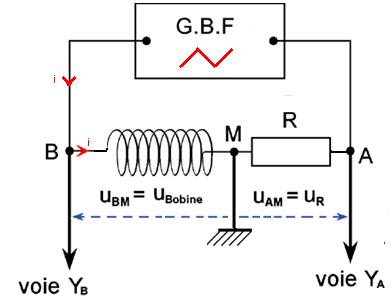
On utilise un oscilloscope qui nous permet de visualiser la tension aux bornes de la résistance et de la bobine sur la voie Y_B  :la tension aux bornes de la bobine Sur la voie Y_A la tension aux bornes de la résistance.

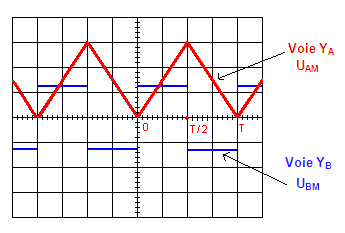
On obtient la courbe représentée ci-dessous

.

l’allure du graphe nous montre  deux tensions :

Sur la voie Y_A on visualise U_AM(t) : tension triangulaire de période T

Sur la voie Y_B on visualise U_BM(t) tension sous forme de  créneaux de période T

Raisonnons théoriquement :

La résistance R nous permet de visualiser l’intensité i(t) dans le circuit

U_AM(t) = R.i(t) = at + b

(a est une constante qui s’exprime en V / s).

Entre les dates 0 et T / 2 : 

U_AM = R.i = a.t + b      (( di / dt )) = a / R

U_BM = u_o  ( u_o > 0 est une constante)

Le rapport                     U_BM / (( di / dt )) = u_o / (a / R) = u_o . R / a

Entre les dates T / 2 et T :

U_AM = R.i = – a.t + b            (( di / dt )) = – a / R

U_BM = – u_o < 0

Le rapport                U_BM / (( di / dt )) = – u_o / (- a / R) = u_o . R / a

Le  rapport  U_BM / (( di / dt )) reste donc constant.

Pour toute variation de  fréquence du signal en dents de scie

Le  rapport  U_BM / (( di / dt )) = L   reste toujours  constant

Donc   L est une caractéristique de la bobine qu’on appelle inductance

L’inductance L s’exprime en V.s / A ou  en henry ( H )

 On constate que  les créneaux obtenus ne sont pas parfaitement horizontaux   cela montre que la bobine a une résistance interne r.

Expression de l’intensité aux bornes d’une bobine

La tension aux bornes d’une bobine:

U_BM=      r i +L di / dt

Réponse d’un dipôle RL à un échelon de tension

  Activité 3

D’après l’activité 1 La bobine retarde l’établissement du courant. On  va étudier ce phénomène.

Comment varie l’intensité du courant dans une bobine (L, r)   soumise à un échelon de tension?

On considère le montage suivant : Un dipôle RL de résistance R et d’une bobine d’inductance  L.

Rôle de la diode en parallèle avec une bobine :

• Ne laisse passer le courant que dans un seul sens

• Évite l’apparition des étincelles dues aux surtensions aux bornes de la bobine

• Protège  les composants du circuit  autour de la bobine

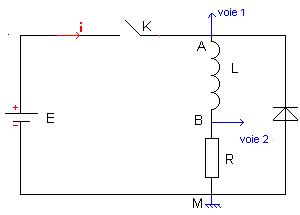
Pour visualiser les tensions : les deux Voie 1 et Voie 2  sont branchés à l’oscilloscope à mémoire

Que visualise-t-on sur la voie 1 ?

Que visualise-t-on sur la voie 2 ?

Observation

Quand on ferme l’interrupteur K  à t=0 Sur l’écran de l’oscilloscope on enregistre les graphes suivants :  

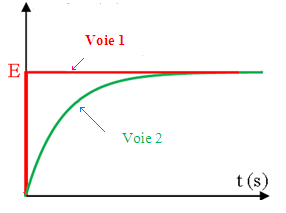
Sur la voie 1,  à t=0  la tension U_AM  = 0 V   Quand  on ferme  l’interrupteur K, cette tension passe brusquement à la valeur E = 12 V . Ce brusque passage de 0 V à E = 12 V s’appelle un échelon de tension.

Sur la voie 2, on observe  U_BM = R i   l’allure de l’évolution de l’intensité du courant i qui augmente progressivement de la valeur nulle jusqu’à la valeur maximale  Imax = E / R après un retard temporel.

On remarque que la présence de la bobine AB retarde l’établissement du courant.

Etude théorique.

a) Equation différentielle :

b) Solution de l’équation différentielle :

La solution de l’équation différentielle s’écrit sous la forme suivante :

On montre, en mathématique, que la solution de cette équation est:

i(t) = Ae^-mt+B

A, B et m sont des constantes.

Détermination de A , B et m

Détermination de B et m

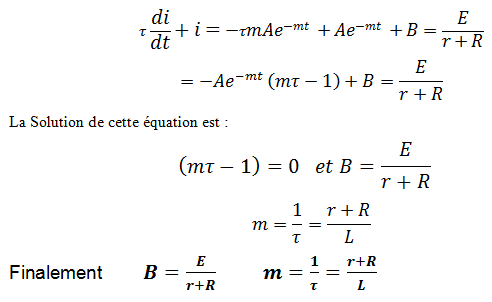
Détermination de la constante A

D’après les conditions  initiales  à t=0    l’intensité du courant dans la bobine est nulle :

donc   i(0) = 0 

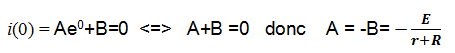
Donc la solution de l’équation différentielle s’écrit sous la forme suivante :

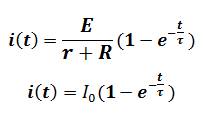
Avec I₀=E/(r+R)

Au moment où l’on ferme l’interrupteur, (à t = 0 on a i (0) = 0)  

En régime permanent, à  t > 5τ         t → +∞    on a i(+∞) =I₀ =E/(r+R)

i(5τ)  = I₀ (1-e^-5) =0,99 I₀

Détermination de la constante du temps  τ =  L/(R+r)

1^ère  méthode

On utilise la solution de l’équation différentielle :

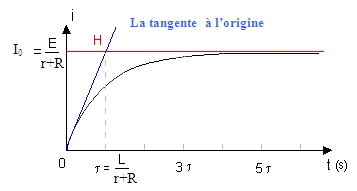
i(τ)  = I₀ (1-e^-1) =0,63I₀    Avec I₀=E/(r+R)

τ est l’abscisse qui correspond à l’ordonnée 0,63 I₀

2^ème  méthode :

utilisation de la tangente à la courbe à l’instant t=0 .

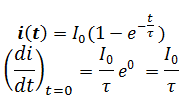
l’équation de la tangente est la droite :

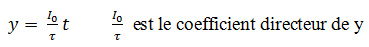
L’expression de la tension aux bornes de la bobine

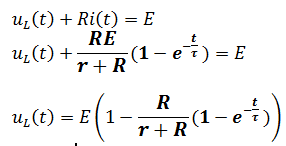
On néglige la résistance de la bobine r  devant R  on a :

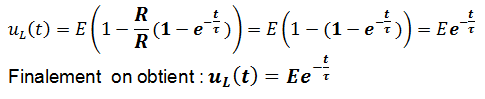
Constante de temps du dipôle RL

Analyse dimensionnelle :

Vérification de l’unité de la constante de temps par analyse dimensionnelle.

Donc      La constante de temps a la dimension d’un temps. Son unité est la seconde (s).

Par lecture graphique de l’abscisse du point de la courbe dont l’ordonnée est égale à 0,63.U0, on obtient la valeur de τ.

La rupture du courant dans une bobine

a) Equation différentielle :

Quand on ouvre K, la tension U_AM passe instantanément de E à 0 (pour t ≥ 0 ⇒ U_AM = 0).

D’après l’additivité des tensions , on a

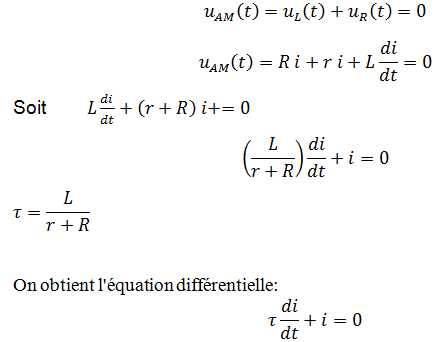
b) Solution de l’équation différentielle :

La solution de l’équation différentielle s’écrit sous la forme suivante :

On montre, en mathématique, que la solution de cette équation est:

i(t) = Ae^-mt+B

A, B et m sont des constantes.

Détermination de A , B et m

Détermination de B et m

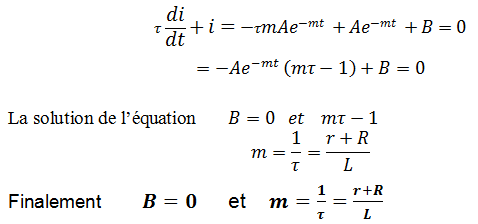
Détermination de la constante A

D’après la condition initiale     à t=0     le courant est donc 

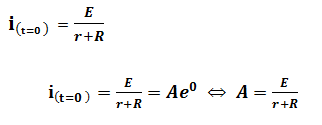
Donc la solution de l’équation différentielle s’écrit sous la forme suivante :

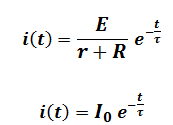
à t= τ   i(τ)  = I₀ e^-1 =0,37 I₀

à t → +∞    pratiquement on considère :  t > 5 τ on a i(+∞) =0

L’énergie stockée dans une bobine

On réalise le montage du circuit suivant   comportant  un moteur , une bobine d’inductance importante et une diode D .

A la fermeture de  l’interrupteur K un courant électrique traverse la bobine  la diode est bloquée.

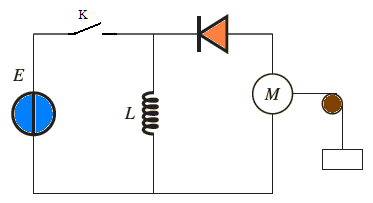
Observation

Lorsque qu’on ouvre  de l’interrupteur, le moteur tourne en soulevant le

Une masse. Comment  explique t- on ce phénomène ?

Interprétation

Cela  montre que la bobine emmagasine de l’énergie à la fermeture de l’interrupteur K;  cette énergie est fournit au moteur sous forme d’une énergie mécanique lors de l’ouverture du circuit ;

L’expression de l’énergie emmagasinée dans une bobine Lorsqu’on ferme le circuit, la loi d’additivité de tension s’écrit :

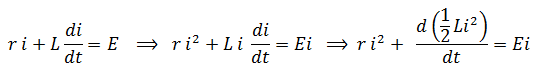
E i  représente la puissance fournit par le générateur au circuit

• r i²  représente la puissance dissipée par effet Joule dans le circuit