Présentation des systèmes oscillants
Un oscillateur mécanique est un système qui effectue un mouvement de va et vient autour de sa position d’équilibre.
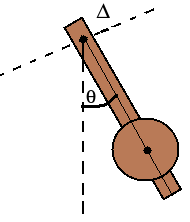
Pendule pesant :
Un pendule pesant est un solide oscillant en rotation autour d’un axe fixe (Δ) horizontal ne passant pas par son centre de gravité G.
exemples : balançoire, balancier d’une horloge
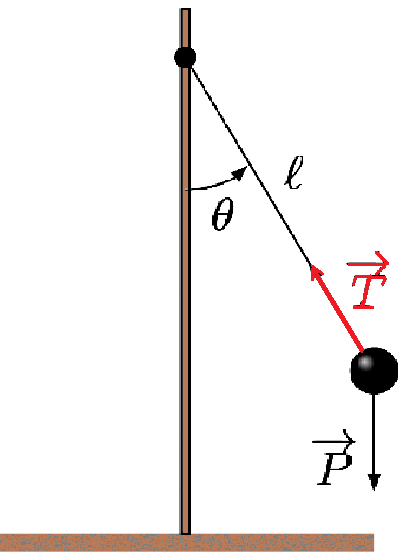
Pendule simple
Un pendule simple est constitué d’un solide ponctuel de masse m accrochant à l’extrémité d’un fil inextensible de longueur l et de masse négligeable devant m.
Le pendule simple constitue un cas particulier du pendule pesant.
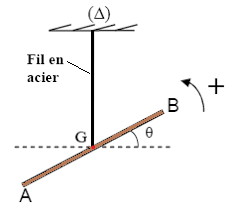
Pendule de torsion
Un pendule de torsion est un dispositif constitué d’une barre horizontale tel que son centre d’inertie est attaché à l’extrémité d’un fil métallique vertical, l’autre extrémité est maintenue fixe à un support.
Pendule élastique
Un pendule élastique est un système (ressort-solide )
Il est constitué d’un ressort de constante de raideur k fixe d’une des extrémités sur un support, l’autre extrémité est reliée à un solide de masse m ses spires ne sont pas jointives et sa masse est négligeable devant la masse du solide
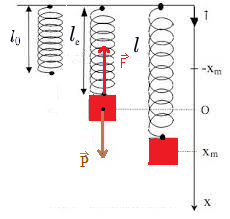
Caractéristiques des mouvements oscillants
Un oscillateur écarté de sa position d’équilibre, il oscille autour de cette position d’équilibre.
Il est dit libre lorsqu’il n’est soumis à aucun apport d’énergie extérieure.
La position du centre d’inertie des pendules pesant, simple et de torsion est repérée par l’abscisse angulaire, pour un pendule élastique, il est repéré par l’abscisse cartésien x (translations rectilignes).
Grandeurs physiques caractérisant un oscillateur
L’amplitude
L’amplitude du mouvement d’un oscillateur libre et non amorti est l’écart maximum positif par rapport à la position d’équilibre stable.
L’amplitude θmax est l’angle maximale en (rad) pour « Pendule pesant, simple et de torsion »
L’ abscisse angulaire θ varie périodiquement entre une valeur minimale –θm et une valeur maximale+θm
L’amplitude xmax est l’allongement maximal d’un ressort en (m)
– Pour « Pendule élastique » : L’abscisse cartésien varie périodiquement entre une valeur minimale -xm et une valeur maximale+xm
L’amplitude du oscillations libres et non amorties reste constante.
La période propre
La période d’un oscillateur libre et non amorti est la durée qui s’écoule entre deux passages successifs de l’oscillateur par sa position d’équilibre stable dans le même sens. Son unité dans SI est la seconde (s).
Les oscillations d’un oscillateur mécanique libre et non amorti sont dites périodiques.
Amortissement des oscillations
Phénomène d’amortissement
Lorsqu’on écarte un oscillateur mécanique de sa position d’équilibre stable, l’amplitude du mouvement diminue jusqu’à l’arrêt du mouvement.On dit que les oscillations s’amortissent progressivement, l’oscillateur est amorti.
Il existe deux types de frottements :
+ Frottement solide : a lieu entre l’oscillateur et un solide «l’amplitude diminue linéairement avec le temps »
+ Frottement fluide: se produit entre l’oscillateur et un fluide (liquide ou gaz) « l’amplitude diminue exponentiellement avec le temps »
Régimes d’amortissement
En absence des frottements: on a un régime sinusoïdal périodique
En cas des faibles frottements, l’amortissement est faible: on a un régime pseudo-périodique
En cas des frottements est très fort , l’amortissement est important, il n’y a plus du tout d’oscillations : on a un régime apériodique.
Étude du pendule élastique horizontal
Le solide de masse m attaché à l’une des extrémités d’un ressort posée sur un support plan horizontal, l’autre extrémité du ressort est fixé à un support fixe.
Les frottements sont considérés comme négligeables.
Pour faire l’étude du centre d’inertie G du solide S on choisit un repère Galiléen l’axe (O ;
)
Au repos Le centre d’inertie G du solide S est en O pris comme l’origine de l’axe (Ox )
On repère la position du centre d’inertie G , à chaque instant par l’abscisse cartésienne x(t)
Force de rappel exercée par un ressort
On écarte le solide de sa position d’équilibre, et on le relâche sans vitesse initiale .
Au repos : la longueur de ressort est ℓ0
le ressort écarte ou comprimé : la longueur de ressort devient ℓ, l’allongement du ressort est alors: Δl = ℓ−ℓ0 =x
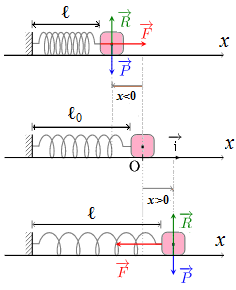
En effet le ressort exerce alors une force de rappel proportionnelle à son allongement.
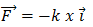
k :Le coefficient de proportionnalité appelé constante de raideur du ressort, (N.m-1).
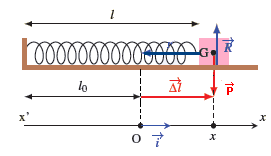
Si le ressort est comprimé, l’allongement x=ℓ−ℓ0 est négatif, alors la force 
=−k(ℓ−ℓ0)=−kx est dirigé dans le sens de l’axe Ox.
Si le ressort est étiré, l’allongement x=ℓ−ℓ0 est positif, alors la force =−k(ℓ−ℓ0)=−kx est dirigé dans le sens inverse de l’axe Ox.
Équation différentielle
– Système : le solide accroché au ressort.
– Référentiel : terrestre supposé galiléen
– Bilan des forces :
: Poids 
: réaction normale au plan : force de rappel du ressort
On applique la deuxième loi de Newton
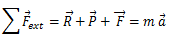
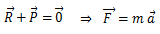
Par projection sur l’axe Ox on trouve:
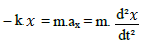
Donc l’équation différentielle s’écrit:
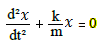
Solution de l’équation différentielle
La solution de cette équation différentielle est de la forme :
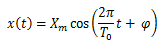
- Xm : amplitude des oscillations, positive en m.
- T0 : période propre des oscillations en s.
- φ : représente la phase à l’origine des dates en radian.
Expression de la période propre T0
On dérive deux fois x(t) par rapport au temps t :
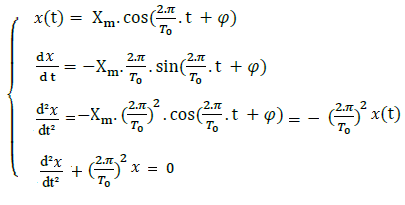
D’après l’équation différentielle: 
et l’expression calculée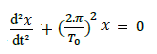 
alors
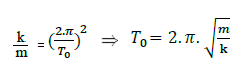
Étude d’un pendule pesant
On considère un pendule pesant constitué d’une tige homogène de masse m qui peut tourner autour d’un axe horizontal (Δ), son moment d’inertie par rapport à (Δ) est JΔ.
On écarte la tige de sa position d’équilibre d’un angle θm , puis on la libère sans vitesse initiale, elle effectue un mouvement de va-et-vient.
Les frottements sont supposés négligeables.
On repère la position du pendule par l’abscisse angulaire θ que fait la tige avec la verticale.
Équation différentielle du mouvement
Système étudié : tige solide
Référentiel : référentiel terrestre supposé Galiléen.
Bilan des forces :: le poids du système : force exercée par l’axe (Δ) sur (S) ;
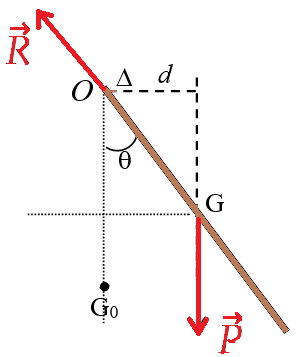
Application de la relation fondamentale de la dynamique :
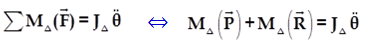
Puisque la droite d’action de 
coupe l’axe (Δ) donc 
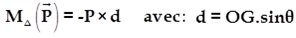
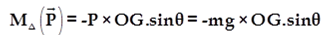
Donc l’équation différentielle s’écrit:
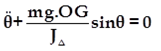
Dans le cas général Le mouvement du pendule pesant est de rotation oscillatoire non sinusoïdale
Pour des faibles oscillations (θ ⩽ 0;26rad) on peut écrire sinθ ≈θ , d’où l’équation différentielle :
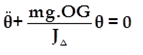
Le mouvement du pendule pesant dans le cas de faibles oscillations est de rotation sinusoïdale
Solution de l’équation différentielle
La solution de cette équation différentielle est de la forme :
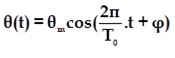
- θm : amplitude des oscillations, une grandeur positive en (rad).
- T0 : la période propre des oscillations en (s).
- φ : la phase à l’origine des dates en radian.
Expression de la période propre T0
On dérive deux fois l’expression θ(t) par rapport au temps t :
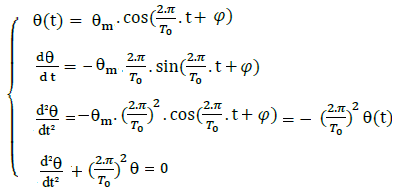
D’après l’équation différentielle: 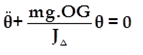et l’expression calculée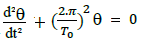 
alors
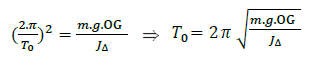
Étude du Pendule simple
Équation différentielle
Le pendule élastique est un cas particulier du pendule pesant ; avec 
et 
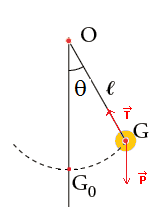
l’équation différentielle s’écrit :
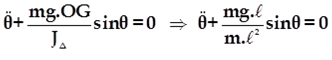
d’où:
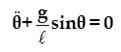
Dans le cas des oscillations de faibles amplitudes , l’équation différentielle s’écrit :
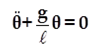
La solution de cette équation différentielle est de la forme :
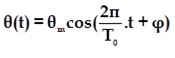
L’expression de la période propre du pendule simple est :
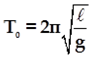
Étude du Pendule de torsion
Couple de rappel exercé par le fil de torsion
Lorsqu’on applique un couple de forces à la tige d’un pendule de torsion , le fil se tord , celui-ci réagit à la torsion en exerçant des forces de rappel équivalentes à un couple de torsion dont le moment par rapport à l’axe Δ a pour expression: MΔ , couple= −C θ .
- C : la constante de torsion du fil (N.m/rad)
- θ : angle de torsion (rad)
- M : moment du couple de torsion (N.m)
Équation différentielle
On écarte de sa position d’équilibre, d’un angle θm , et on la lâche sans vitesse initiale.
On néglige tous les frottements.
Le système composé du « fil métallique +tige » effectue des oscillations libres autour de sa position d’équilibre.
Soit JΔ le moment d’inertie de la tige par rapport à l’axe de rotation Δ
On étudie le mouvement dans le référentiel terrestre considéré Galiléen
Les positions de la tige sont repérés à chaque instant par l’abscisse angulaire θ (t)
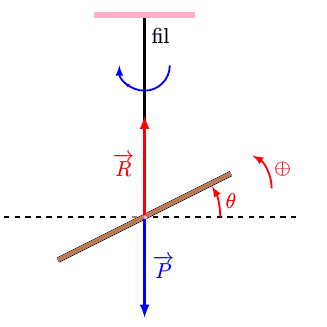
La tige est soumise à deux forces 
et 
au couple de torsion MC= −C θ.
D’après la relation fondamentale de la dynamique:
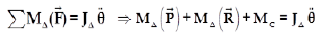
Puisque et coupent l’axe de rotation , donc: 
D’où:
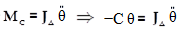
Donc l’équation différentielle s’écrit::
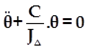
Solution de l’équation différentielle
La solution de cette équation différentielle est de la forme :
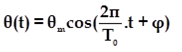
- θm : représente l’amplitude des oscillations, une grandeur positive en (rad)
- .T0 : représente la période propre des oscillations en (s)
- .φ : représente la phase à l’origine des dates en radian
Expression de la période propre T0
On dérive deux fois l’expression θ(t) par rapport au temps t :
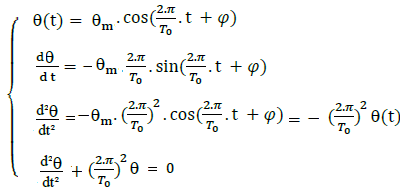
D’après l’équation différentielle: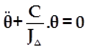
et l’expression calculée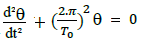
alors
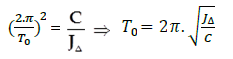
Oscillation forcée et résonance
Définition
Un système oscillant, appelé résonateur oscille naturellement à sa fréquence propre fo = 1 / To , s’il oscille à la fréquence f imposée par un excitateur, on dit qu’il subit des oscillations forcées.
Expérience :
Une des extrémités d’un pendule élastique attaché à un solide (S) immergeant dans l’eau, l’autre extrémité du pendule élastique est accrochée à un fil passant par la gorge d’une poulie et fixé à un disque tournant
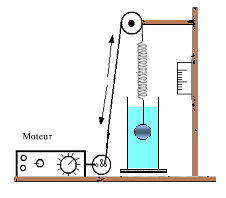
Au moment où le disque tourne, le pendule élastique effectue des oscillations forcées à la fréquence f imposée par le disque.
Lorsqu’on augmente lentement la fréquence f de l’excitateur on observe que:
- L’amplitude des oscillations du pendule élastique dépend de la fréquence f de l’excitateur.
- L’amplitude est maximale quand la fréquence f de l’excitateur est proche de la fréquence propre f0 (f ≈ f0) On dit que le résonateur entre en résonance.
Conclusions
Lorsqu’un système oscillant est excité à une fréquence voisine de sa fréquence propre f0 : La résonance se manifeste, l’amplitude des oscillations est maximale
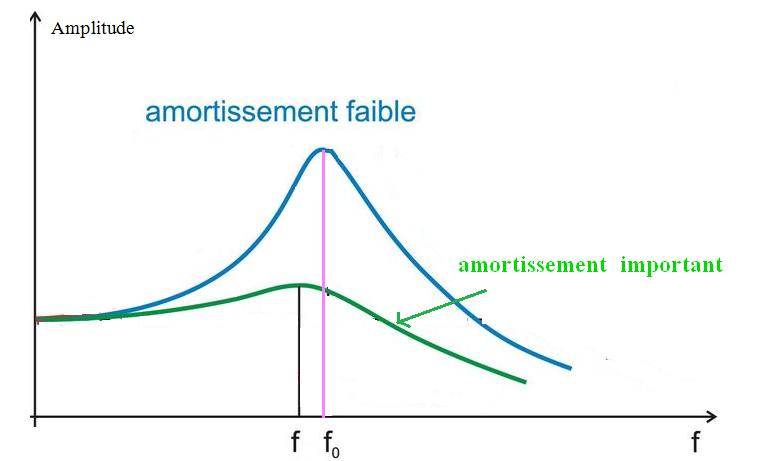
Influence de l’amortissement sur la résonance :
Pour un amortissement faible du résonateur, l’amplitude des oscillations forcées à la résonance prend une valeur grande ; on dit que la résonance est aigüe.
Pour un amortissement important du résonateur, l’amplitude des oscillations prend une valeur faible, on dit que la résonance est floue.
