Voici un cours complet : le dipôle RC pour le terminale Français.
Table of Contents
Le comportement d’un condensateur dans un circuit électrique
1) La charge électrique sur les armatures
Activité 1
On réalise un circuit qui comporte :
Un condensateur, un générateur de tension continue, un interrupteur, une lampe des appareils de mesure : « voltmètre et ampèremètre »
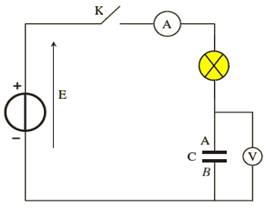
Qu’observez-vous à la fermeture de l’interrupteur k ?
Observation
A la fermeture de l’interrupteur k, on constate que :
- La lampe s’allume immédiatement et s’éteint très rapidement.
- Apparition d’un courant maximal dans le circuit
- Le voltmètre indique une augmentation de la tension entre les deux armatures A et B du condensateur alors que l’ampèremètre montre une diminution d’intensité,
- En fin la tension aux bornes du condensateur atteint E « tension au borne du générateur » alors que l’intensité s’annule.
- La tension entre les armatures persiste sur la valeur E.
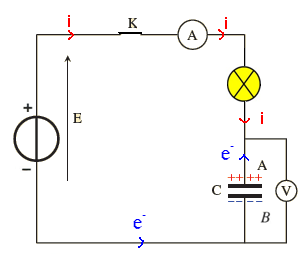
Interprétation
Le passage du courant est du à un déplacement d’électrons dans le circuit.
Dans notre circuit, l’intensité du courant circule en direction de l’armature A depuis le générateur ; alors que les électrons circulent en sens inverse, vers l’armature B.
Donc au cours de cette charge, Les électrons quittent l’armature A et se charge positivement qA > 0 tandis que l’armature B fixe Les électrons et se charge négativement: qB < 0
A chaque instant, qA = – qB Ces charges s’expriment en coulomb (C).
Puisque la charge électrique se conserve donc les armatures A et B portent des charges électriques opposées, de même valeurs absolues à chaque instant.
La tension électrique qui apparaît entre les armatures et qui persiste montre que le condensateur est chargé.
Conclusion
Un condensateur, branché à un générateur de tension continue, accumule sur ses armatures des charges électriques de même valeur, mais de signes opposés.
2)Relation entre Charge électrique et intensité
- Cherchons la relation entre l’intensité i et les charges électriques qA et qB
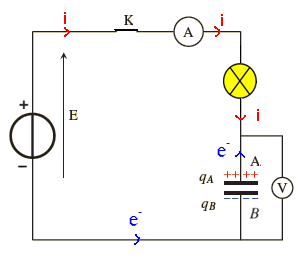
Dans notre circuit i > 0 l’intensité du courant qui circule en extérieur du générateur (+) en direction de A;
Durant un temps dt , l’armature A perd des électrons alors que l’armature B les reçoit ceci implique que :
Entre les instants t et t+dt, qA augmente de : dqA = qA(t+dt) – qA(t) >0
dqA = – dqB = dq
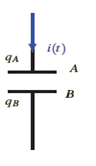
qA(t) , qB(t) sont des fonction du temps en régime transitoire.
Par définition, l’intensité i du courant est le débit de charge électrique, circulant dans le circuit par unité de temps et par section unité
Donc i =dq/dt= dqA /dt= – dqB /dt
L’intensité i s’exprime en ampère (A) , avec q en coulomb (C) et t en seconde (s) .
3) La capacité d’un condensateur
On Charge un condensateur avec un courant continu I débité par un générateur de courant.
Comment évolue la tension UAB aux bornes des armatures A et B du condensateur en fonction de la charge électriques des armatures qA?
Étude expérimentale
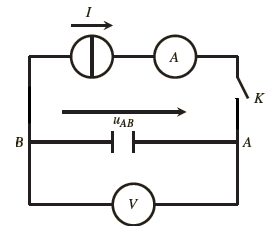
On réalise le montage avec un générateur de courant continu fixé à une intensité constante
I = 100μA.
Le condensateur est déchargé.
On ferme l’interrupteur en même temps que le déclenchement du chronomètre.
On mesure la tension uAB au bornes du condensateur chaque 10 secondes.
On enregistre les résultats dans le tableau suivant :
| t (s) | 0 | 10 | 20 | 30 | 40 | 50 |
| uAB (V) | 0 | 0,5 | 1,00 | 1,5 | 2,5 | 8,41 |
| q (μC) |
Puisque l’intensité est constante et égale à I=100μA d’où la relation :
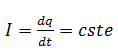
La charge du condensateur est : qA = I × t + q0
Le condensateur est initialement déchargé alors q0 =0 donc qA = I × t
on complète le tableau ci-dessous en calculant la charge par la relation : qA = I × t
| t (s) | 0 | 10 | 20 | 30 | 40 | 50 |
| uAB (V) | 0 | 0,5 | 1,00 | 1,5 | 2,5 | 8,41 |
| qA (μC) | 0 | 1 | 2 | 3 | 4 | 5 |
On représente la courbe qA = f (uAB)
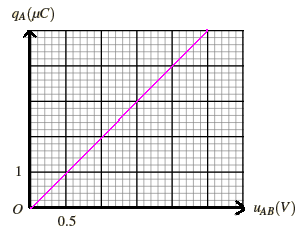
La courbe qA = f (uAB) est une droite linéaire
Donc : qA(t) = C × uAB(t)
Le coefficient de proportionnalité positif C est la capacité du condensateur.
La charge électrique qA de l’armature A du condensateur est proportionnelles à la tension uAB aux bornes de ses armatures A et B à chaque instant: qA(t) = C × uAB(t)
C :capacité du condensateur; exprime en farad (F), avec qA en coulomb et uAB en volt (V).
Association des condensateurs
Association en parallèle
Condensateurs en parallèle : plusieurs condensateurs en parallèle se comportent comme un unique condensateur de capacité équivalente à Céq telle que :
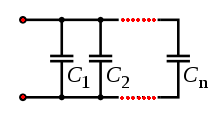
Céq=C1 +C2+……. Cn
Pour deux condensateurs C1 et C2 en parallèle :
Céq=C1 +C2
Condensateurs en série : plusieurs condensateurs en série se comportent comme un unique condensateur de capacité équivalente à Céq telle que :
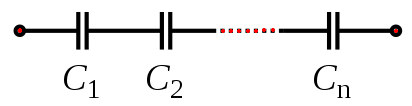
Pour deux condensateurs C1 et C2 en série :
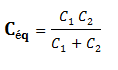
La réponse d’un dipôle RC à un échelon de tension
Etude expérimentale
L’étude de l’évolution de la charge électrique du condensateur lorsque la tension entre les bornes d’un dipôle RC passe de 0 à une valeur constante E; appelée un échelon de tension.
Activité 3
Réaliser le montage suivant :
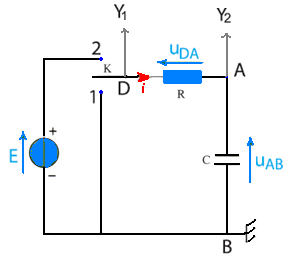
- Les voies Y1 et Y2 sont branchées sur un oscilloscope à mémoire
- Mettre l’interrupteur sur la position 2
- Vos observations sur les tensions uDB , uDB etuAB ?
Observation
Sur la voie Y1 la tension uDB est passée instantanément d’une valeur 0 à une valeur constante égale à E
Sur la voie Y2 la tension uAB aux bornes du condensateur augmente progressivement de la valeur nulle jusqu’à la valeur maximale égale à E après un retard temporel.
la tension uAB décrit l’évolution de la charge du condensateur qA = C . uAB
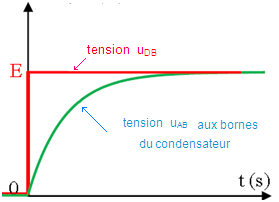
Entre les voies Y1 et Y2 tension aux bornes du conducteur ohmique:
uDA =uDB – uAB = R. i la tension est proportionnelle à l’intensité i
D’après la courbe, l’intensité i du courant est égale à zéro avant la fermeture de l’interrupteur, après la fermeture de l’interrupteur l’intensité i est égal à E/R. cette intensité décroit ensuite jusqu’à zéro.
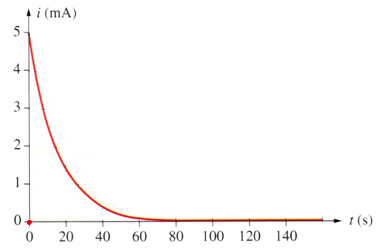
Conclusion
Le condensateur d’un dipôle RC , soumis à un échelon de tension, se charge progressivement avec un retard temporel, donc la charge d’un condensateur est un phénomène transitoire.
2) La constante de temps
Selon le dipôle RC choisi, la tension UAB aux bornes des armatures tend plus ou moins rapidement vers sa valeur limite E. de même qA = C . UAB
Quels sont les paramètres influents sur le phénomène de charge?
Si on associe une résistance plus grande à notre circuit : le condensateur se charge plus lentement
De même Si on associe une un condensateur de plus grande capacité : le condensateur se charge plus lentement.
La durée de charge du condensateur d’un dipôle RC augmente quand la valeur du produit R.C augmente.
Analyse dimensionnelle du produit R.C en raisonnant sur les unités :
R = U/I s’exprime en Ohm , équivalent à V/A;
C = Q/U = I.t / U s’exprime en Farad (F) équivalent à A.s /V
En fin : R.C s’exprime en V/A.A.s/V, soit en seconde (s).
Le produit τ = R.C , est la constante de temps du dipôle s’exprime en seconde (s), R en Ohm et C en farad (F).
3) étude théorique
Le condensateur est orienté de l’armature A vers l’armature B,
Pour simplifier les notations :
Pour la charge du condensateur qA = q la tension UAB = UC
Tension au borne de la résistance R UDA = UR
Reprenons le circuit électrique précèdent plus simplifié utilisé lors de l’étude de la charge du condensateur:
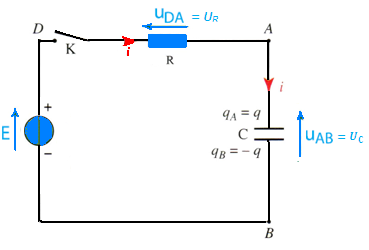
On applique la loi d’additivité des tensions:
E = uC +uR
E = R . i + uC avec la loi d’Ohm : uR = Ri
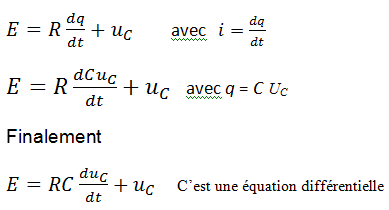
Solution de l’équation différentielle
On montre, en mathématique, que la solution de cette équation est:
uc = Ae-mt+B
A, B et m sont des constantes.
Détermination de A , B et m
1ère étape conditions initiales à t=0 Le condensateur est vide donc uC (0) = 0.
uC (0) =Ae0+B=0 <=> A+B =0 donc B =- A d’où uC = Ae-mt -A
2ème étape à t → +∞ le condensateur est complètement chargé : uC (+∞) = E.
uC (+∞)= Ae-∞ -A =E <=> -A= E d’où A=-E Donc uC = E – E e-mt
3ème étape
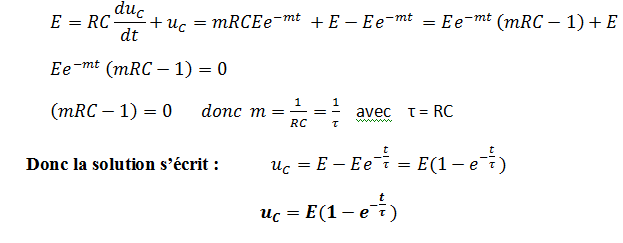
τ est appelée constante de temps du dipôle RC.
Au moment où l’on ferme l’interrupteur, la tension aux bornes du condensateur est nulle (à t = 0 on a uC (0) = 0) et il s’établit un courant i0=E/R
En régime permanent, à t > 5τ 0 ( t → +∞ on a uC(+∞) =E) le condensateur est chargé donc pas de mouvement de charges et i=0,
uC(5τ) = E(1-e-5) =0,99E
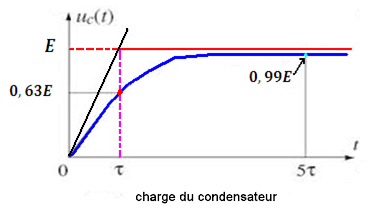
Détermination de la constante du temps τ = RC
1ère méthode
On utilise la solution de l’équation différentielle :
uC(τ) = E(1-e-1) =0,63E
τ est l’abscisse qui correspond à l’ordonnée 0,63E
2ème méthode :
utilisation de la tangente à la courbe à l’instant t=0 .
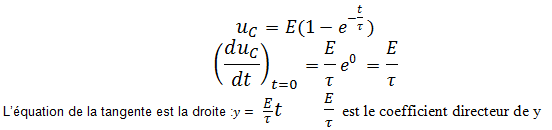
Expression de l’intensité du courant de charge
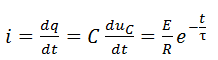
La décharge d’un condensateur à travers une résistance
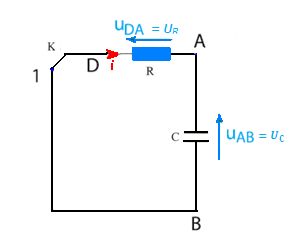
à t=0 le condensateur est chargé, uc(0)=E, on ferme l’interrupteur K.
d’après la loi des mailles : uR + uc = 0 avec uR =Ri
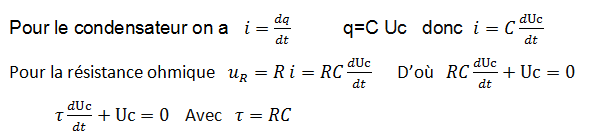
Solution de l’équation différentielle
uc = Ae-mt+B
A, B et m sont des constantes. Déterminons A , B et m
1ère étape :
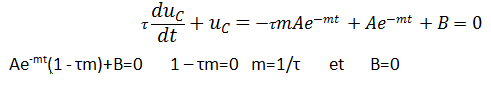
2ème étape :
à t=0 état où le condensateur est chargé . uC (0) = E
uC (0) = Ae0 = E d’où A = E
donc la solution de l’équation différentielle s’écrit : uC = E e-t /τ
à t= τ uC(τ) = E e-1 =0,37E
A l’instant où l’on bascule l’interrupteur (à t = 0) la tension aux bornes du condensateur
vaut uC (0) = E et il s’établit un courant i0=E/R et quand t → +∞ on a uC = 0 , pratiquement on considère : t > 5 τ on a uC(+∞) =0 le condensateur est déchargé et plus de mouvement de charges donc la tension et l’intensité s’éteignent.
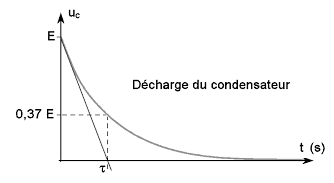
Expression de l’intensité du courant de décharge
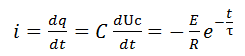
C’est Intensité du condensateur au cours de la décharge électrique.
L’énergie stockée dans un condensateur
Expression de l’énergie électrique emmagasinée dans le condensateur
La puissance délivrée par le générateur au condensateur est :
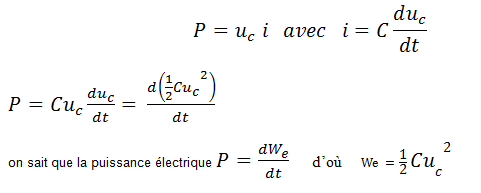
L’énergie électrique stockée par un condensateur est égal à
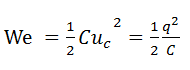
We s’exprime en joule (J) avec C en farad (F), UC en volt et q en coulomb (C)







