Mouvements Plans : Cours Complet

Mouvement d’un projectile dans un champ de pesanteur uniforme

Lancement d’un projectile

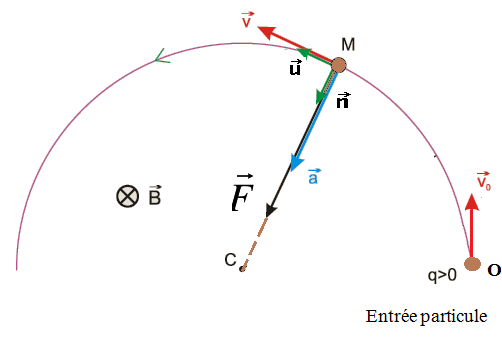
A partir d’un point O, et à l’ instant t = 0, On lance une balle de tennis de masse m, de centre d’inertie G, avec une vitesse initiale v0 faisant un angle α par rapport à l’horizontale.

A l’aide d’une webcam , on réalise l’enregistrement du mouvement de balle de tennis .

Etudions le mouvement dans l’espace champ de pesanteur 𝐠⃗ uniforme .

Observations :

les positions du centre d’inertie G de balle de tennis évoluent sur le plan vertical (Oxy) donc le mouvement est plan

Le vecteur vitesse du centre d’inertie change de valeurs et de direction au cours du mouvement.
Le vecteur accélération est vertical descendant, constant, la direction et sens est celui du vecteur champs de pesanteur

Bilan des forces extérieures :

Le projectile de masse 𝑚 placé dans le champ de pesanteur 𝐠⃗ subit une force de pesanteur représentée par un vecteur P = m 𝐠⃗ , son mouvement est accéléré suivant l’axe Oy

D’après la seconde loi de Newton :.

$\sum_{} \vec{F_{ext}} = m \vec{a_{G}} = \vec{P} = m \vec{g} \Leftrightarrow \vec{a_{G}} = \vec{g}$

$l ‘ acceleration \vec{a_{G}} a pour expression \vec{a_{G}} = - g \vec{j}$

Les coordonnés du vecteur accélération sont:

$\vec{a_{G}} {\begin{cases} a_{x} = o \\ a_{y} = - g \\ a_{z} = o \end{cases}$

Conditions initiales :
Le projectile est lancé depuis le point origine O, le vecteur vitesse initial V0 faisant un angle α avec le plan horizontal (xOy) .

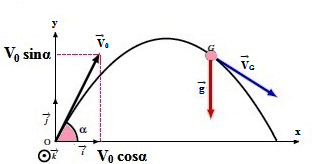
A t = 0, le vecteur vitesse initiale du centre d’inertie G est:

$\vec{V_{o}} = V_{o} cosα \vec{i} + V_{o} sinα \vec{j}$

les coordonnées des vecteurs: (position et vitesse) du centre d’inertie G à la date t=0 sont respectivement :

$\vec{{OG}_{o}} {\begin{cases} x (o) = o \\ y (o) = o \\ z (o) = o \end{cases} et \vec{V_{o}} {\begin{cases} V_{x} (o) = V_{o} cosα \\ V_{y} (o) = V_{o} sinα \\ V_{z} (o) = o \end{cases}$

Équations horaires du vecteur vitesse

A la date t quelconque , les vecteurs vitesse et accélération sont:

$\vec{V_{G}} = V_{x} \vec{i} + V_{y} \vec{j} + V_{z} \vec{k} et \vec{a_{G}} = \frac{d \vec{V_{G}}}{dt} = \frac{{dV}_{x}}{dt} \vec{i} + \frac{{dV}_{y}}{dt} \vec{j} + \frac{{dV}_{z}}{dt} \vec{k}$

${\begin{cases} a_{x} = \frac{{dV}_{x}}{dt} = o \\ a_{y} = \frac{{dV}_{y}}{dt} = - g \\ a_{z} = \frac{{dV}_{z}}{dt} = o \end{cases} \Rightarrow {\begin{cases} V_{x} (t) = \int a_{x} dt = C_{1} \\ V_{y} (t) = \int a_{y} dt = - gt + C_{2} \\ V_{z} (t) = \int a_{z} dt = o \end{cases}$

$à t = o on a : {\begin{cases} V_{x} (o) = V_{o} cosα = C 1 \\ V_{y} (o) = V_{o} sinα = C 2 \\ V_{z} (o) = o \end{cases}$

Finalement les coordonnées du vecteur vitesse sont:

${\begin{cases} V_{x} (t) = V_{o} cosα \\ V_{y} (t) = - gt + V_{o} sinα \\ V_{z} (t) = o \end{cases}$

Équations horaires du vecteur position

les coordonnées du vecteur vitesse s’écrit également

${\begin{cases} \frac{dx}{dt} = V_{x} (t) = V_{o} cosα \\ \frac{dy}{dt} = V_{y} (t) = - gt + V_{o} sinα \\ \frac{dz}{dt} = V_{z} (t) = o \end{cases}$

Pour trouver l’expression de coordonnée position on calcule les primitifs des ordonnées vitesse:

${\begin{cases} x (t) = \int V_{o} cosαdt = V_{o} \cos (α) t + C_{1} \\ y (t) = \int - gt + V_{o} sinα = - \frac{1}{2} {gt}^{2} + V_{o} \sin (α) t + C_{2} \\ z (t) = \int V_{z} dt = o \end{cases}$

$à t = o {\begin{cases} x (o) = C_{1} = o \\ y (o) = C_{2} = o \\ z (o) = o \end{cases} donc {\begin{cases} x (t) = V_{o} cosαt \\ y (t) = - \frac{1}{2} {gt}^{2} + V_{o} sinαt \\ z (t) = o \end{cases}$

Finalement les coordonnées du vecteur position OG sont :

${\begin{cases} x (t) = V_{o} \cos (α) t \\ y (t) = - \frac{1}{2} {gt}^{2} + V_{o} \sin (α) t \\ z (t) = o \end{cases}$

Équation de la trajectoire du projectile

Pour obtenir une équation de la trajectoire, il faut exprimer y(t) en fonction x(t).

Éliminons le paramètre t, en utilisant l’équation horaire x(t) établie précédemment:

$x (t) = V_{o} \cos (α) t \Rightarrow t = \frac{x}{V_{o} cosα}$

En introduisant cette expression dans la seconde équation horaire, On obtient alors:

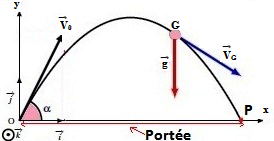
$y = - \frac{1}{2} g \frac{x^{2}}{V_{o}^{2} {\cos (α)}^{2}} + \frac{V_{o} \sin (α)}{V_{o} \cos (α)} x$

$on simplifie l ‘ équation y = - \frac{1}{2} g \frac{x^{2}}{V_{o}^{2} {\cos (α)}^{2}} + tang (α) x$

Détermination de la portée

La portée est l’abscisse x_pdu point P, dont l’ordonnée y_p est nulle. C’est le point du sol sur lequel arrive le projectile après sa chute.On appelle portée la distance maximale horizontalement parcourue par le projectile, . la valeur de la portée x_p est calculé lorsque y(x) = 0.

Ceci conduit à résoudre l’équation y = 0, soit

$y = - \frac{1}{2} g \frac{x^{2}}{V_{o}^{2} {\cos (α)}^{2}} + tang (α) x = O$

$(- \frac{g}{2 V_{o}^{2} {\cos (α)}^{2}} . x + tangα) . x = O$

En factorisant par x on montre qu’il existe deux solutions :
• la solution x = 0 qui correspond au point de lancer O,
• l’autre solution : xp et qui vérifie

$- \frac{g}{2 V_{o}^{2} {\cos (α)}^{2}} . x_{p} + \frac{sinα}{cosα} = O$

$x_{p} = \frac{2 V_{o}^{2} sinα cosα}{g} o r 2 sinα cosα = \sin 2 α donc x_{p} = \frac{V_{o}^{2} \sin 2 α}{g}$

Finalement la portée est égale à :

$OP = x_{p} = \frac{V_{o}^{2} \sin (2 α)}{g}$

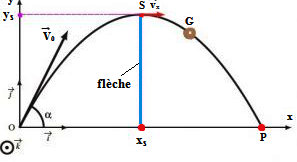
Détermination de la flèche

On appelle la flèche l’altitude maximale y_S atteinte par G donc le projectile est au sommet S de sa trajectoire, la composante verticale de la vitesse est nulle : V_y = 0 et la tangente à la courbe en S est horizontale, donc dy/dx = 0

Première méthode de la détermination y_S :

$Exploitons les 2 equations V_{y} (t) = - gt + V_{o} sinα et y (t) = - \frac{1}{2} {gt}^{2} + V_{o} \sin (α) t$

$V_{y} (t_{s}) = - {gt}_{s} + V_{o} sinα = o \Rightarrow t_{s} = \frac{V_{o} sinα}{g} y (t_{s}) = - \frac{1}{2} g {t_{s}}^{2} + V_{o} \sin (α) t_{s} = - \frac{1}{2} g {(\frac{V_{o} sinα}{g})}^{2} + \frac{{(V_{o} sinα)}^{2}}{g} = \frac{V_{o}^{2} \sin^{2} α}{2 g}$

Finalement la flèche a pour expression:

$y_{s} = \frac{V_{o}^{2} \sin^{2} α}{2 g}$

Deuxième méthode de la détermination y_S

$\frac{dy}{dx} = \frac{d}{dx} (- \frac{1}{2} g \frac{x^{2}}{V_{o}^{2} \cos^{2} α} + tang (α) . x) = \frac{g}{V_{o}^{2} \cos^{2} α} x + tang (α)$

${(\frac{dy}{dx})}_{x_{s}} = \frac{g}{V_{o}^{2} \cos^{2} α} x_{s} + tang (α) = 0 \Leftrightarrow x_{s} = \frac{V_{o}^{2} sinα cosα}{g}$

L’abscisse du sommet S de la trajectoire est x_S, ainsi la flèche de la trajectoire est y_S

$y_{s} = - \frac{g}{2 V_{o}^{2} {\cos (α)}^{2}} x_{s}^{2} + tang (α) . x_{s} = \frac{V_{o}^{2} \sin^{2} α}{2 g}$

Mouvement d’une particule chargée dans un champ électrique uniforme

Condensateur plan

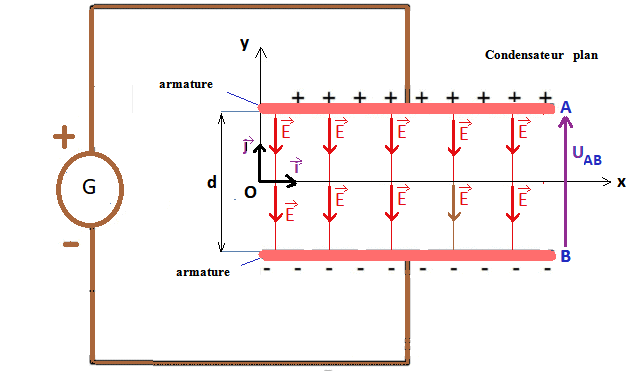
Un condensateur plan est composé de deux armatures conductrices planes parallèles, de longueur L et espacées d’une distance d.

Champ électrique d’un condensateur plan

A l’aide d’un générateur on applique une différence de potentiel constante entre 2 armatures.

Les armatures sont portées à deux potentiels, l’une est chargée positivement et l’autre négativement.

Les armatures sont portées à deux potentiels, l’une est chargée positivement et l’autre négativement.

En effet un champ électrique E ⃗ uniforme règne entre les armatures, son expression est la suivante, dans le repère ( O,i,j )

$(O, \vec{i}, \vec{j}) \vec{E} = - \frac{U_{AB}}{d} \vec{j}$

La direction champ électrique E ⃗ est perpendiculaire à la surface des armatures ; orientée de la plaque positive vers la plaque négative

(dirigée vers les potentiels décroissants de A vers B : V_A > V_B Sa norme constante est donnée par la relation : E = U/d (en V/m)

La force électrique (force de Coulomb)

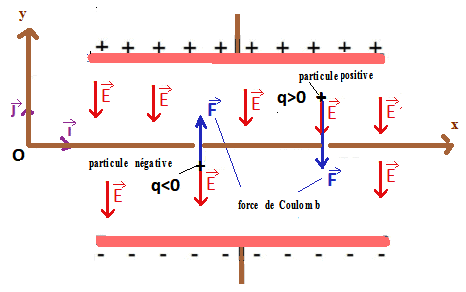
Considérons une particule chargée placée entre les armatures d’un condensateur plan à air soumis à une différence de potentiel.

Nous remarquons que la particule subit force électrostatique

toute particule de charge placée entre les armatures subit la force de Coulomb dont l’expression est :

$\vec{F} = q \vec{E}$

F ⃗ est donc colinéaire à E ⃗ et le sens dépend du signe de la charge:

Si q > 0, alors F et E sont dans le même sens.
Si q < 0, alors F et E sont dans des sens opposés.
Si q = 0, alors la force électrique est nulle.

Particule chargée en mouvement dans un champ électrique uniforme

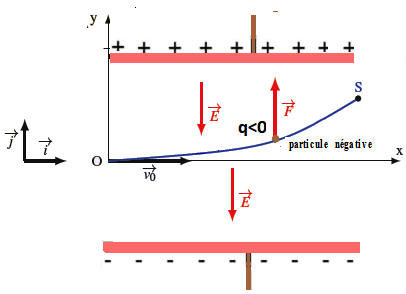
On considère à l’instant t = 0 une particule de charge q et de masse m, entre dans le champ d’un condensateur plan en O , avec une vitesse initiale v₀horizontale. ( un champ électrique E constant entre les deux armatures plan règne )

Etudions le mouvement du particule au sein champ électrique

Système : {particule de charge q, de masse m}

Référentiel : Terrestre galiléen, repère orthonormé cartésien (O,i,j,k)

Bilan des forces extérieures :

le poids est toujours négligeable pour les particules
$Force électrique est \vec{F} = q \vec{E}$

D’après la seconde loi de Newton:

$\vec{F} = m \vec{a} \Leftrightarrow m \vec{a} = q \vec{E} \Leftrightarrow \vec{a} = \frac{q}{m} \vec{E}$

Equations horaire du système

Coordonnées du vecteur accélération de la particule:

$\vec{a_{G}} {\begin{cases} a_{x} (t) = o \\ a_{y} (t) = - \frac{qE}{m} \\ a_{z} (t) = o \end{cases}$

Coordonnées du vecteur vitesse de la particule:

$\vec{V_{G}} {\begin{cases} V_{x} (t) = V_{o} \\ V_{y} (t) = - \frac{qE}{m} t \\ V_{z} (t) = o \end{cases}$

Coordonnées du vecteur position:

$\vec{OG} {\begin{cases} x (t) = V_{o} t \\ y (t) = - \frac{qE}{2 m} t^{2} + V_{o} t \\ z (t) = o \end{cases}$

Équation de la trajectoire

La trajectoire de la particule est contenue dans le plan (Oxy).

En éliminant le temps t entre les deux équations x(t) et y(t)

Il faut donc éliminer le paramètre temps t des équations horaires x(t) et y(t) :

$y = - \frac{qE}{2 m . V_{o}^{2}} x^{2}$

Cette équation cartésienne est celle d’une parabole

Etudions le mouvement du particule après sa sortie du champ électrique

Au delà du point S les particules chargés ne sont soumis à aucune force

donc le mouvement est rectiligne uniforme, d’après le principe d’inertie,

Les coordonnées du point S à la sortie du condensateur sont :

$\vec{OS} {\begin{cases} x_{s} = l \\ y_{s} = - \frac{qE}{2 V_{o}^{2} m} l^{2} \\ z_{s} = o \end{cases}$

La date de passage de la particule par le point S est t =l / v0

Les coordonnées La vitesse Vs de la particule à la sortie au point S

$\vec{V} {\begin{cases} V_{Sx} = V_{o} \\ V_{Sy} = - \frac{qE}{m} . \frac{l}{V_{o}} \\ V_{Sz} = o \end{cases}$

Le vecteur Vs⃗ forme avec l’horizontal un angle de déviation angulaire α , tel que:

$tanα = \frac{V_{Sy}}{V_{Sx}} = - \frac{qE l}{{mV}_{o}^{2}}$

Déviation électrique

À la sortie du champ électrique , le mouvement de la particule est

rectiligne uniforme de vitesse jusqu’à ce qu’il heurte l’écran au point O.

On appelle déflexion électrique la distance De entre le point d’impact A’ de la particule avec l’écran en absence du champ électrique et le point d’impact A de la particule avec l’écran en présence du champ électrique.

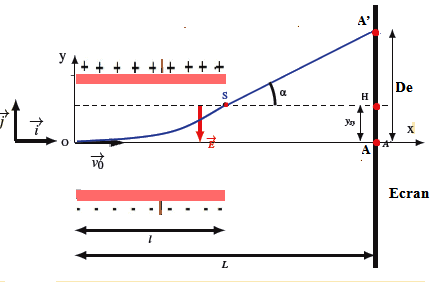
De = A′A = A′H+HA=( L-l ) tanα +y_s

$De = - (L - \frac{l}{2}) . \frac{qE l}{{mV}_{0}^{2}}$

$on sait que E = \frac{U}{d} alors De = - (L - \frac{l}{2}) . \frac{qUl}{{mdV}_{0}^{2}}$

la déflexion électrique est proportionnelle à la tension entre les plaques elle est sous la forme : De= k U

$a v e c K = - (L - \frac{l}{2}) . \frac{ql}{{mdV}_{o}^{2}}$

Cette propriété est utilisée dans le principe de fonctionnement d’un oscilloscope

Mouvement d’une particule chargée dans un champ magnétique uniforme

Force magnétique : Force de Lorentz

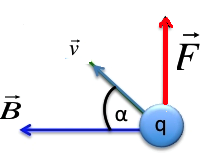
une particule de charge q est en mouvement avec une vitesse V⃗ dans un champ magnétique uniforme de vecteur B⃗ , une force magnétique appelée force de Lorentz F⃗ donnée par:

$\vec{F} = q \vec{v} \land \vec{B}$

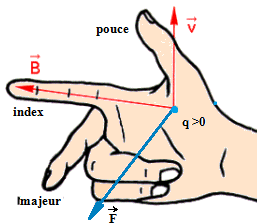
Caractéristiques de la force de Lorentz

Point d’application : la particule chargée
Direction : la droite perpendiculaire au plan formé par q𝑣 ⃗ et 𝐵⃗ )
Sens : il est donnée par la règle des trois doigts de la main droite la main droite
Intensité : F = |q v B . sin( 𝑎 )|
α est l’angle formé par q𝑣 ⃗ et 𝐵⃗

Etude cinématique d’une particule chargée dans un champ magnétique uniforme

Une charge électrique q < 0 de masse m est introduite en un point O avec la vitesse initiale 𝑣⃗ , dans un espace où règne un champ magnétique uniforme 𝐵⃗ et perpendiculaire au vecteur 𝑣₀.

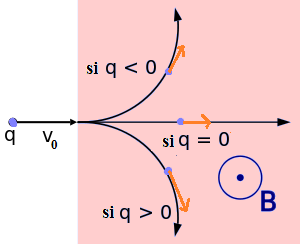
On étudie le mouvement de la particule

Le système étudié : { la particule}
Référentiel : Base de Frenet
Bilan des forces :Force de Lorentz, (le poids de la particule est négligeant devant la force de Lorentz)

Application de la deuxième loi de Newton

$\vec{F} = m \vec{a} = q \vec{v} \land \vec{B} d o n c \vec{a} = \frac{q}{m} \vec{v} \land \vec{B}$

on déduit que le vecteur accélération a de la particule, est perpendiculaire au vitesse à tout instant

Projection de vecteur accélération a sur les axes du repère de Frenet est:

$\vec{a} = \vec{a_{T}} + \vec{a_{N}} = a_{T} \vec{u} + a_{N} \vec{n} = \frac{dv}{dt} \vec{u} + \frac{v^{2}}{ρ} \vec{n} P u i s q u e \vec{a} p e r p e n d i c u l a i r e à \vec{v} d o n c a_{T} = \frac{dv}{dt} = 0$

La vitesse tangentiel à la trajectoire est constant alors le mouvement est uniforme

la force de Lorentz 𝐹⃗ est porté par le vecteur unitaire 𝑛 ⃗

on dit que la force est centripète

$\vec{a} = a_{N} \vec{n} = \frac{v^{2}}{ρ} \vec{n} \frac{v^{2}}{ρ} = \frac{| q |}{m} v . B \Rightarrow ρ = \frac{mv}{| q | . B}$

Puisque m, v, q et B sont constants donc ρ : le rayon de courbure de la trajectoire est constant ( ρ=R) alors le mouvement est circulaire.

Conclusion : toute particule chargée entrant dans un champ magnétique avec une vitesse perpendiculaire à 𝑩⃗ décrit un mouvement t circulaire uniforme perpendiculaire au champ 𝑩⃗ Le rayon de la trajectoire est donné par l’expression suivante:

$R = \frac{mv}{| q | . B}$

Voir aussi: Mouvement de rotation d’un solide autour d’un axe fixe