Repérage dans l’espace

Coordonnées dans l’espace

Définition :

Un repère dans l’espace est déterminé par un point  O (origine du repère) et un triplet (𝒊⃗ , 𝒋⃗ ,𝒌⃗), de vecteurs non coplanaires appelé base de vecteurs. On le note (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗)

  𝒊⃗= OI  , 𝒋⃗ = OJ   , 𝒌⃗=OK    le repère est dit orthonormé lorsque les droites (OI) , (OJ),  (OK) sont deux à deux perpendiculaires et OI=OJ=OK=1

• la droite (OI) est l’axe des abscisses, la droite (OJ) est l’axe des ordonnées et la droite (OK) est l’axe des côtes.

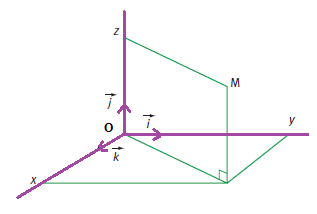
Coordonnées d’un point

Pour tout point de l’espace, il existe un unique un unique triplet (x ; y ; z ) de réels tels que : 

$\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$

Coordonnées d’un vecteur

A tout vecteur 𝒖⃗ on peut associer un unique triplet (x ; 𝒚 ; z ) tel que:

$\overrightarrow{u}=x\overrightarrow{i}\mathit{+}y\overrightarrow{j}+z\overrightarrow{k}$

 Ce triplet (x ; 𝒚 ; z ) est appelé coordonnées du point  M ou de vecteur  𝒖⃗

Représentation paramétrique d’une droite de l’espace

L’espace est muni d’un repère orthonormé (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗) .

On considère la droite (D ) passant par le point  A(x_A ; y_A ; z_A) et de vecteur directeur  𝒖⃗( 𝜶 ; 𝜷; 𝜸).

L’ensemble des points M ( x; y; z ) appartient à (D ) si et seulement s’ il existe un réel t tel que : 

$\overrightarrow{\mathbf{AM}}\mathbf{=}\mathbf{t}\overrightarrow{\mathbf{u}}\mathbf{ }\mathbf{ }\mathbf{avec}\mathbf{ }\mathbf{t}\mathbf{\in }\mathbf{ℝ}$

 

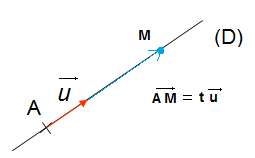
Équation vectorielle d’une droite

Soit A(x_A ; y_A ; z_A) un point de la droite (D) pour tout point M (x;y;z )∈(D) 

$\overrightarrow{\mathrm{AM}} \mathrm{est} \mathrm{une} \mathrm{équation} \mathrm{vectorielle} \mathrm{de} \mathrm{la} \mathrm{droite} \mathrm{D} \mathrm{passant} \mathrm{par} \mathrm{le} \mathrm{point} \mathrm{A} \mathrm{et} \mathrm{de} \mathrm{vecteur} \mathrm{directeur} \overrightarrow{u}$

$\mathrm{Les} \mathrm{coordonnées} \mathrm{du} \mathrm{vecteur} \overrightarrow{\mathrm{AM}} \mathrm{sont} : (x–x_A;y-y_A;z-z_A)$

 Les coordonnées du vecteur 𝒖⃗  sont : ( 𝜶 ; 𝜷; 𝜸)

$\overrightarrow{\mathbf{AM}}\mathbf{=}\mathit{t}\overrightarrow{\mathbf{u}}\mathbf{ }\mathbf{\iff }\mathbf{ }\mathbf{\left(}\begin{array}{c}\mathbf{x}\mathbf{-}{\mathbf{x}}_{\mathbf{A}}\\ \mathbf{y}\mathbf{-}{\mathbf{y}}_{\mathbf{A}}\\ \mathbf{z}\mathbf{-}{\mathbf{z}}_{\mathbf{A}}\end{array}\mathbf{\right)}\mathbf{=}\mathit{t}\mathbf{ }\mathbf{\left(}\begin{array}{c}\mathbf{\alpha }\\ \mathbf{\beta }\\ \mathbf{\gamma }\end{array}\mathbf{\right)}\mathbf{ }\mathbf{\iff }\mathbf{\{}\begin{array}{l}\mathbf{x}\mathbf{=}{\mathbf{x}}_{\mathbf{A}}\mathbf{+}\mathbf{t\alpha }\\ \mathbf{y}\mathbf{=}{\mathbf{y}}_{\mathbf{A}}\mathbf{+}\mathbf{t\beta }\\ \mathbf{z}\mathbf{=}{\mathbf{z}}_{\mathbf{A}}\mathbf{+}\mathbf{t\gamma }\end{array}\mathbf{ }\mathit{o}\mathit{ù}\mathbf{ }\mathit{t}\mathbf{ }\mathit{e}\mathit{s}\mathit{t}\mathbf{ }\mathit{u}\mathit{n}\mathbf{ }\mathit{r}\mathit{é}\mathit{e}\mathit{l}$

  Ce sont des équations paramétriques de la droite (D ) de vecteur directeur 𝒖⃗( 𝜶 ; 𝜷; 𝜸) passant par le point A(x_A ; y_A ; z_A)

Représentation paramétrique d’un plan

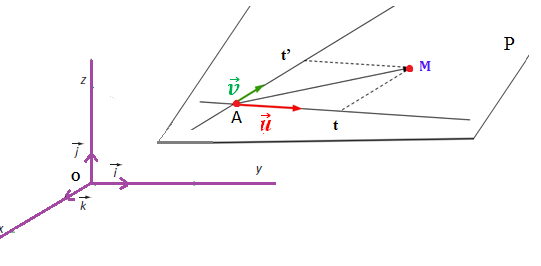
L’espace est muni d’un repère orthonormé (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗),

Soit P un plan de l’espace passant par le point A(x_A ; y_A ; z_A) et de vecteurs directeurs   𝒖⃗ (∝;𝜷;𝜸) et 𝒗⃗(𝜶’;𝜷’;𝜸’)

M ( x; y; z ) appartient au plan P et seulement si, il existe deux réels t et  t’ tels que: 

$\overrightarrow{\mathit{AM}}\mathit{=}\mathbf{t}\overrightarrow{\mathit{u}}\mathit{+}\mathbf{t}\mathit{‘}\overrightarrow{\mathit{v}}$

$\mathrm{Les} \mathrm{coordonnées} \mathrm{du} \mathrm{vecteur} \overrightarrow{\mathrm{AM}} \mathrm{sont} : (x–x_A;y-y_A;z-z_A)$

Les coordonnées du vecteur 𝒖⃗ sont :(𝜶 ; 𝜷; 𝜸)

Les coordonnées du vecteur 𝒗⃗ sont :(𝜶’ ; 𝜷’; 𝜸’)

$\mathbf{ }\overrightarrow{\mathbf{AM}}\mathit{=}\mathit{t}\overrightarrow{\mathbf{u}}\mathit{+}\mathit{t}\mathit{‘}\overrightarrow{\mathbf{v}}\mathbf{\iff }\mathbf{\left(}\begin{array}{c}\mathbf{x}\mathbf{-}{\mathbf{x}}_{\mathbf{A}}\\ \mathbf{y}\mathbf{-}{\mathbf{y}}_{\mathbf{A}}\\ \mathbf{z}\mathbf{–}{\mathbf{z}}_{\mathbf{A}}\end{array}\mathbf{\right)}\mathbf{=}\mathit{t}\mathbf{ }\mathbf{\left(}\begin{array}{c}\mathbf{\alpha }\\ \mathbf{\beta }\\ \mathbf{\gamma }\end{array}\mathbf{\right)}\mathbf{+}\mathit{t}\mathbf{‘}\mathbf{ }\mathbf{\left(}\begin{array}{c}\mathbf{\alpha }\mathbf{‘}\\ \mathbf{\beta }\mathbf{‘}\\ \mathbf{\gamma }\mathbf{‘}\end{array}\mathbf{\right)}\mathbf{\iff }\mathbf{\{}\begin{array}{l}\mathbf{x}\mathbf{=}{\mathbf{x}}_{\mathbf{A}}\mathbf{+}\mathbf{t}\mathbf{ }\mathbf{\alpha }\mathbf{+}\mathbf{t}\mathbf{‘}\mathbf{ }\mathbf{\alpha }\mathbf{‘}\\ \mathbf{y}\mathbf{=}{\mathbf{y}}_{\mathbf{A}}\mathbf{+}\mathbf{t}\mathbf{ }\mathbf{\beta }\mathbf{+}\mathbf{t}\mathbf{‘}\mathbf{ }\mathbf{\beta }\mathbf{‘}\\ \mathbf{z}\mathbf{=}{\mathbf{z}}_{\mathbf{A}}\mathbf{+}\mathbf{t}\mathbf{ }\mathbf{\gamma }\mathbf{+}\mathbf{t}\mathbf{‘}\mathbf{ }\mathbf{\gamma }\mathbf{‘}\end{array}$

où t et t’ sont des réels.

Ce sont des équations paramétriques du plan de vecteurs directeurs 𝒖⃗(𝜶; 𝜷;𝜸) et 𝒗( 𝜶’ ; 𝜷’; 𝜸’) et passant par le point A de coordonnées A(x_A ; y_A ; z_A)

 

Produit scalaire dans l’espace

Produit scalaire du plan

Propriétés du produit scalaire

• 𝒖⃗. 𝒗⃗ =𝒗⃗ .𝒖⃗
• (𝒖⃗ +𝒗⃗ ) . 𝒘⃗ = 𝒖⃗ . 𝒘⃗ + ⃗𝒗 . 𝒘⃗  et  𝒖⃗.( 𝒗⃗ + 𝒘⃗ ) = 𝒖⃗ . ⃗𝒗 + 𝒖⃗ . 𝒘⃗
• 𝒖⃗ ² = 𝒖⃗. 𝒖⃗ = ‖𝒖⃗ ‖²

Identités remarquables :

• ‖𝒖⃗ +𝒗⃗ ‖² = (𝒖⃗ +𝒗⃗)² = 𝒖⃗ ² +2𝒖⃗ .𝒗⃗ +𝒗⃗ ² = ‖𝒖⃗ ‖² + 2𝒖⃗ .𝒗⃗ +‖𝒗⃗ ‖²
• ‖𝒖⃗ -𝒗⃗ ‖²= (𝒖⃗ – 𝒗 ⃗ )² = 𝒖⃗ ²– 2𝒖⃗ . 𝒗⃗ +𝒗⃗ ² = ‖𝒖⃗ ‖² – 2𝒖⃗. 𝒗⃗ + ‖𝒗⃗ ‖²
• (𝒖⃗ + 𝒗⃗ ) (𝒖⃗ – 𝒗⃗ ) = 𝒖⃗ ² – 𝒗⃗ ² = ‖𝒖⃗ ‖² – ‖𝒗⃗ ‖²

Produit scalaire dans l’espace

Expression analytique du produit scalaire

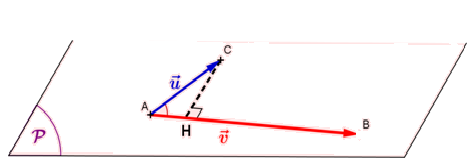
𝒖⃗. 𝒗⃗ = ‖𝒖⃗ ‖ × ‖𝒗⃗ ‖ × 𝒄𝒐𝒔 (𝒖⃗ ;𝒗⃗ )

Si dans un plan 𝓟, H est le projeté orthogonal de C sur (AB) alors :

𝒖⃗. 𝒗⃗ = 𝑨⃗𝑩 . 𝑨⃗𝑪 = 𝑨⃗𝑩 . 𝑨⃗𝑯

• 𝒖⃗. 𝒗⃗ = 𝟏/2 (‖𝒗⃗ + 𝒖⃗ ‖² − ‖𝒖⃗ ‖² − ‖𝒗⃗‖²)

Dans un repère orthonormé de l’espace (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗), si deux vecteurs 𝒖⃗ et 𝒗⃗ ont pour coordonnées respectives (𝒙 ; 𝒚 ; 𝒛) et (𝒙′; 𝒚′ ; 𝒛’), alors :𝒖⃗ . 𝒗⃗ = 𝒙𝒙’ + 𝒚𝒚’ +𝒛𝒛’

 

Orthogonalité dans l’espace

vecteurs orthogonaux

Définition:

Dans l’espace, dire que deux vecteurs 𝒖⃗ et 𝒗⃗ non nuls sont orthogonaux signifie que si 𝒖⃗ = 𝑨𝑩⃗ et 𝒗⃗ = 𝑨⃗𝑪  alors les droites (AB) et (AC) sont orthogonales.

𝒖⃗ et 𝒗⃗ sont orthogonaux si et seulement si  𝒖⃗.𝒗⃗ = 0

Dans un repère orthonormé de l’espace (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗), 𝒖⃗ et 𝒗⃗ ont pour coordonnées respectives (𝒙 ; 𝒚 ; 𝒛) et (𝒙′; 𝒚′ ; 𝒛’) 𝒖⃗ et 𝒗⃗ sont orthogonaux si et seulement si 𝒙𝒙’ + 𝒚𝒚’ +𝒛𝒛’ = 𝟎

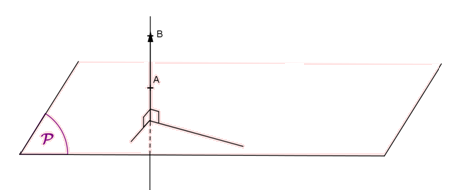
vecteur normal à un plan

Un vecteur AB non nul, est normal à un plan P signifie que la droite( AB) est perpendiculaire à ce plan

 

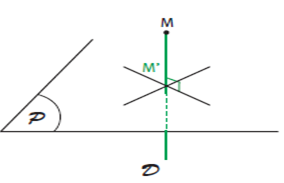
Projection orthogonale sur un plan

Définition:

Soit P un plan et M un point de l’espace. La droite perpendiculaire à P passant par M coupe le plan P en M ^′ appelé projeté orthogonal de sur P

 

Équation cartésienne d’un plan en fonction d’un vecteur normal

Vecteur normal à un plan

Théorème : Un vecteur non nul n⃗ est normal à un plan si, et seulement si, il est orthogonal à deux vecteurs non colinéaires de ce plan

Equation cartésienne d’un plan

Théorème : Etant donné un point A(x_A ; y_A ; z_A) et un vecteur non nul

n⃗ , l’ensemble des points M de l’espace tels que:

$\overrightarrow{n}.\overrightarrow{AM}=0 \mathrm{est} \mathrm{le} \mathrm{plan} \mathrm{contenant} \mathrm{A} \mathrm{et} \mathrm{de} \mathrm{vecteur} \mathrm{normal} \overrightarrow{\mathrm{n}}$

 soient  M(x ; y ; z)∈P   et A(x_A ; y_A ; z_A)

$\mathrm{Les} \mathrm{coordonnées} \mathrm{du} \mathrm{vecteur} \overrightarrow{\mathrm{AM}} \mathrm{sont} : (x–x_A;y-y_A; z-z_A)$

n⃗ ⊥ A⃗M ⟺ n⃗. A⃗M = 0 ⟺ a(𝑥 − 𝑥_𝐴) + b(𝑦 − 𝑦_𝐴) + c(𝑧 − 𝑧_𝐴) = 0

⟺ax + a 𝑥_𝐴 + by + b 𝑦_𝐴 + cz + c 𝑧_𝐴 = 0

ax + by + cz + (-a 𝑥_𝐴 – b 𝑦_𝐴 – c 𝑧_𝐴 )= 0  posons d egal à la constante : d= –a 𝑥_𝐴 – b 𝑦_𝐴 – c 𝑧_𝐴

Le plan passant par le point A(x_A ; y_A ; z_A) et de vecteur normal n⃗ (a ; b ; c) a pour équation : ax + by + cz +d = 0

Théorème : Tout plan admet une équation de la forme ax + by + cz + d = 0, avec a, b et c non tous nuls, Le vecteur n⃗ (a,b, c) est alors normal à ce plan

Distance d’un point à un plan

Definition

L’espace est rapporté à un repère orthonormé  (𝑶 ; 𝒊⃗ , 𝒋⃗ ,𝒌⃗) .

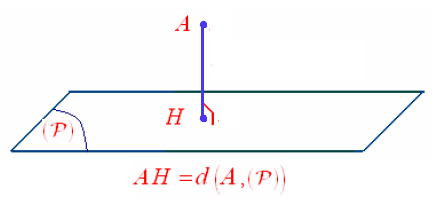
Considérons un point A(x_A ; y_A ; z_A) de l’espace sa projection orthogonal  sur le plan P est H

On appelle A H La distance du point A au plan (P) , notée d(A,(P)) c’est la distance minimale entre A et un point du plan.

Theoreme

Soit (P) le plan d’équation cartésienne a.x+b.y+c.z+d = 0 et  A(x_A; y_A; z_A)  un point de l’espace.

La distance du point A au plan (P)  est  donnée par :

$AH=d(A,(P\left)\right)=\frac{\left|a{x}_A+b{y}_A+c{z}_A+d\right|}{\sqrt{a^2+b^2+c^2}}$

 

La sphère

Définition

La sphère (S) de centre Ω et de rayon R est l’ensemble des points M de l’espace tels que ΩM= R 

  M(x, y, z) ∈(S) ⟺ΩM = R

 

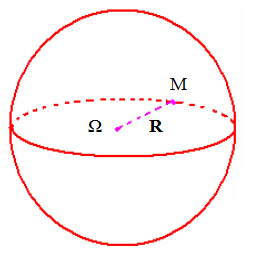
Equation d’une sphère définie par son centre et son rayon.

Soit Ω(x_Ω , y_Ω , z_Ω ) un point dans l’espace et R ≥ 0

M(x, y, z) ∈ (S) ⟺ ΩM = R ⟺ ΩM² = R² ⟺ (x – x_Ω )² + (y – y_Ω )² + (z – z_Ω )² = R²  est une équation cartésienne de la sphère de centre Ω(x_Ω , y_Ω , z_Ω ) et de rayon R

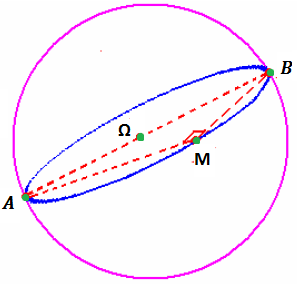
La sphère définie par son diamètre.

Soient Aet B deux points distincts dans l’espace . la sphère de diamètre [𝐴𝐵] est l’ensemble des points 𝑀 dans l’espace qui vérifient :

$\overrightarrow{AM}.\overrightarrow{BM}=0$

Soient (𝑥_𝐴, 𝑦_𝐴, 𝑧_𝐴) et (𝑥_𝐵, 𝑦_𝐵, 𝑧_𝐵) coordonnées de deux points distincts dans l’espace A et B.

$\mathrm{Les} \mathrm{coordonnées} \mathrm{du} \mathrm{vecteur} \overrightarrow{\mathrm{AM}} \mathrm{sont} : (x–x_A;y-y_A; z-z_A)$

$\mathrm{Les} \mathrm{coordonnées} \mathrm{du} \mathrm{vecteur} \overrightarrow{BM} \mathrm{sont} : (x–x_B);(y-y_B);(z-z_B)$

$\overrightarrow{AM}.\overrightarrow{BM}=0\iff (x–x_A)(x–x_B)+( y-y_A)(y-y_B)+(z-z_A)(z-z_B)=0$

C’est une équation de la sphère de diamètre [AB]

 

POSITIONS RELATIVES D’UNE SPHERE ET D’UN PLAN.

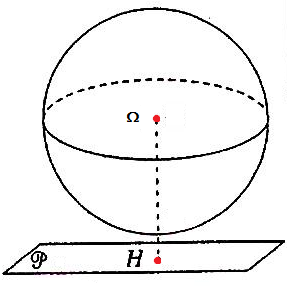
Soit dans l’espace un plan (P) et un sphère (S) de centre Ω de rayon R .

H est la projection orthogonale de Ω sur le plan (P), d est la distance entre le point Ω et le plan (P) noté : d(𝛀, (𝑷)) = 𝛀𝑯 =𝒅

• Si (𝛀, (𝑷)) = 𝛀𝑯 = d < R

Dans ce cas le plan coupe la sphère suivant un cercle de centre r tel que:

r² = R² – d²

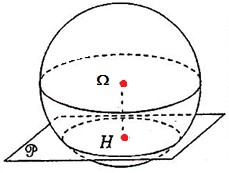
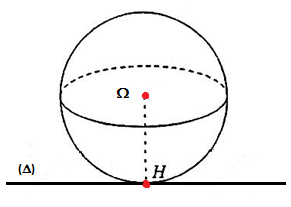
• Si (𝛀, (𝑷)) =𝛀𝑯 =d = R

Dans ce cas le plan est tangent à la sphère en un point H

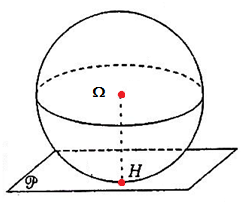
• Si (𝛀, (𝑷)) =𝛀𝑯 =d > R

Donc , tous les point du plan (𝑃) sont à l’extérieure de la sphère

 

L’équation du plan tangent à l’un de ses points.

Soit la sphère (S) de centre Ω et A un de ses points ; si (P) est le plan tangent à 𝑆 en A alors A est la projection orthogonale de Ω sur (𝑃), et donc

$\overrightarrow{\Omega A} \mathrm{est} \mathrm{normal} \mathrm{sur} \left(P\right) \mathrm{par} \mathrm{suite} \mathrm{pour} \mathrm{tout} \mathrm{point} \mathrm{M} (x,y,z)\in \left(P\right)\iff \overrightarrow{AM}.\overrightarrow{A\Omega }=0$

Position relative d’une sphère et d’une droite

la sphère de centre Ω et de rayon R et (Δ) une droite de l’espace

H est la projection orthogonale de Ω sur la droite (Δ) , d est la distance entre le point Ω et la droite (Δ)

• Si 𝛀𝑯 =d < R

Dans ce cas la droite coupe la sphère en deux points

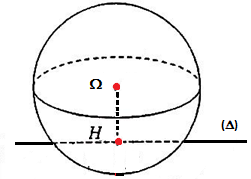
• Si 𝛀𝑯 =d > R

Dans ce cas la droite ne coupe pas à la sphère

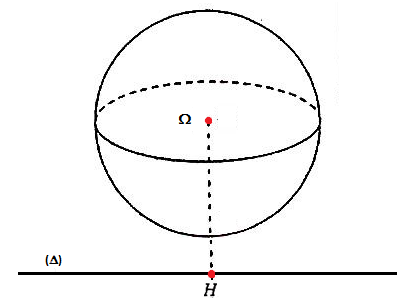
• Si 𝛀𝑯 =d = R

Dans ce cas la droite est tangente à la sphère en un point H