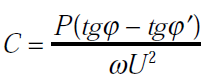Courant alternatif triphasé: Cours de Sciences de l’ingénieur pour: Sciences et Technologies Electrique (STE) , science math STE, BAC S électrotechnique,
Sciences de l’Ingénieur 2ème année du cycle de Baccalauréat
Grandeurs variables périodiques
- Une grandeur variable : évolue au cours du temps ;
- une grandeur périodique :se reproduit identiquement à elle-même à intervalle de temps régulier,
Exemple : u ou u(t) : tension, i ou i(t) intensité ; elles sont notées en minuscules.
- On peut les visualiser avec un oscilloscope
- Elles sont représentées sur l’ordonnée d’un graphique dont l’abscisse est le temps.

Période
La période est la durée constante T, exprimée en seconde, qui sépare deux instants consécutifs, où la grandeur se répète identique à elle-même u(t+T) = u(t)
Fréquence
La fréquence du signal est le nombre de périodes par secondes. Elle est égale à l’inverse de la période. f = 1/T s’exprime en en Hertz (Hz). (1 Hz = 1 s-1)
Valeur instantanée
La valeur instantanée est la valeur de la grandeur variable qu’elle prend à tout instant notée par une minuscule : u(t) ou u , i(t) ou i
Valeur moyenne
La valeur moyenne d’une grandeur de période T est: 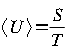
S surface décrite par U(t) sur une période T.
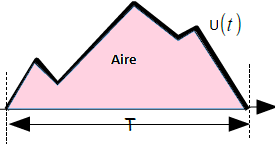
Signal alternatif
Un signal est dit alternatif si sa valeur moyenne est nulle.
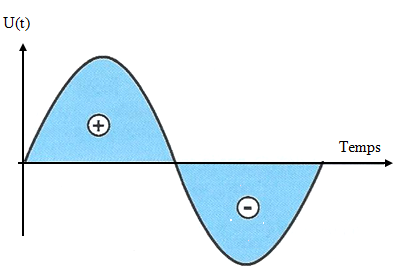
Valeur efficace
La valeur efficace d’une grandeur périodique u est : 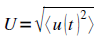
intensité efficace
On appelle intensité efficace, notée I, du courant variable i, l’intensité du courant
continu qui dissiperait la même énergie dans la même résistance pendant la même durée.
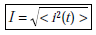
Grandeurs alternatives sinusoïdales
Une grandeur alternative sinusoïdale est une grandeur périodique dont l’équation est une fonction sinusoïdale du temps.
L’expression temporelle de la tension est : u(t) = Umax sin (ωt + φ)
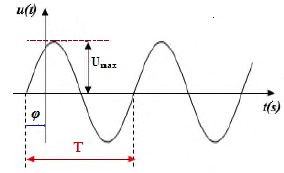
- u(t) : la valeur instantanée de la tension.
- ωt + φ : la phase à l’instant t exprimée en radian.
- φ : la phase à l’origine (t=0).
- ω : vitesse angulaire en rad/s, ω = 2πf = 2π/T.
- Umax : valeur maximale de u
Relation entre valeur efficace et valeur maximale :
Umax = U √2
- U: valeur efficace de u mesurée par un voltmètre AC« .
Représentation de FRESNEL
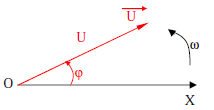
C’est la représentation graphique d’une grandeur sinusoïdale u(t) = U √2 sin (ωt + φ) par l’intermédiaire d’un vecteur de Fresnel, tournant avec la même vitesse angulaire ω du signal sinusoïdal u(t) .
- U : norme du vecteur Fresnel U égale la valeur efficace de u(t)
- φ :angle orienté entre l’axe OX et le vecteur Fresnel
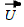 appelé phase à l’origine (t=0)
appelé phase à l’origine (t=0)
Représentation par un nombre complexe
A une grandeur sinusoïdale u(t), on associe une grandeur complexe U. tel que : U = [U ; φ].
- U: module de U c’est la valeur efficace de u(t)
- φ: argument de U c’est la phase à l’origine de u(t).
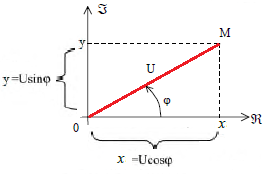
u = U√2 sin (ωt + φ) ↔ U = (U ; φ) = U.cos φ + j U.sin φ
Déphasage
- u(t) = U √2 sin ( ωt + φu),
- i(t) = I √2 sin ( ωt + φi).
On appelle déphasage φ de la tension u par rapport au courant i, la différence entre la phase à l’origine φu de u et la phase à l’origine φi de i φ = φu – φi
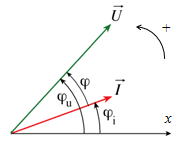
- si φu > φi alors φ > 0 on dit que i est en retard par rapport à u.
- si φu < φi alors φ < 0 on dit que : i est en avance sur u
- φ = 0 : u et i sont en phase
- φ = π : u et i sont en opposition de phase
- φ = π/2 : i est en quadrature retard par rapport à u
- φ= −π/2 : i est en quadrature avance par rapport à u
Loi d’Ohm en régime sinusoïdal
On considère un dipôle D passif, linéaire alimenté en régime sinusoïdal.
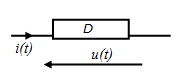
Puisque le dipôle est linaire, si u(t) est sinusoïdale de fréquence f, alors l’intensité du courant qui le traverse est aussi sinusoïdale et de même fréquence.
Les expressions des grandeurs u(t) et i(t) :
- u(t) = U √2 sin ( ωt + φu),
- i(t) = I √2 sin ( ωt + φi).
Enoncé
Pour un dipôle linéaire, alimenté en régime sinusoïdal à fréquence f donnée :
- Le rapport Z = U/I des valeurs efficaces de u(t) et i(t) est appelée impédance du dipôle et s’exprime en Ohm ; il est est constant
- φ = φu – φi est le déphasage de la tension u par rapport à l’intensité i est constant
Conséquence :
A une fréquence donnée, le dipôle D est caractérisé par Z et φ
L’impédance d’un complexe se définit par :
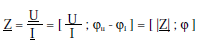
Son admittance complexe est :
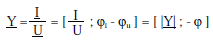
Y s’exprime en Siemens (S)
Dipôles élémentaires
Tout dipôle D passif et linéaire , vu comme un groupement constitué d’un ou plusieurs dipôles
élémentaires. Les dipôles passifs élémentaires sont : la résistance, l’inductance, le condensateur.
La résistance
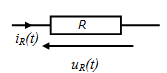
- uR(t) = UR. √2 sin ( ωt + φu)
- iR(t) = IR. √2 sin ( ωt + φi)
sachons que uR(t) = R. iR(t)
UR. √2 sin ( ωt + φu) = R. IR. √2 sin ( ωt + φi) alors UR = R.IR et φu= φi
Résultat
- L’impédance ZR du dipôle est: ZR = UR/IR = R
- Le déphasage de la tension par rapport à l’intensité est nul φ= φu – φi = 0 donc u et i sont en phase
- L’impédance complexe Z vérifie : Z = [R ; 0] = R. Il s’agit d’un nombre complexe purement réel.
Le diagramme de Fresnel donne :
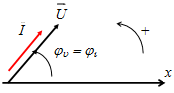
U et I sont colinéaires.
Le condensateur
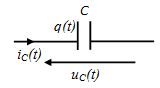
uC(t) et iC(t) s’expriment de la façon suivante :
- uC(t) = UC. √2 sin ( ωt + φi)
- iC(t) = IC. √2 sin ( ωt + φu)
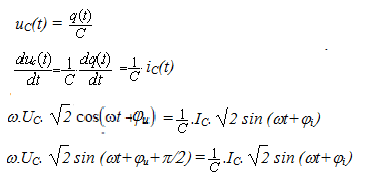
Cette relation implique les deux égalités suivantes :
IC = C ω.UC et φi =φu+π/2
Résultat:
- L’impédance ZC s’exprime par : ZC = UC/IC = 1/Cω
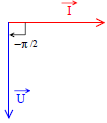
- le déphasage de la tension par rapport à l’intensité du courant φ= φu – φi = –π/2 donc i est en quadrature avance par rapport à u
Impédance complexe d’un condensateur est :
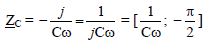
Bobine
sachons que uL(t) = L..![]()
- uL(t) = UL. √2 sin ( ωt + φu)
- iL(t) = IL. √2 sin ( ωt + φi)
alors UL. √2 sin ( ωt + φu) =Lω. IL. √2 cos( ωt + φi)
UL. √2 sin ( ωt + φu) =Lω. IL. √2 sin ( ωt + φi +π/2)
Cette relation implique les deux égalités suivantes :
UL = L ω.IL et φu=φi +π/2
Résultat:
- L’impédance ZL s’exprime par ZL = UL/IL = Lω
- Le déphasage de la tension par rapport à l’intensité du courant φu–φi =π/2 donc i est en quadrature retard par rapport à u

U est en quadrature avance sur I
L’impédance complexe ZL vérifie : ZL = [Lω ; π/2] =jLω
Association de dipôles en série
Dipôle R-L série
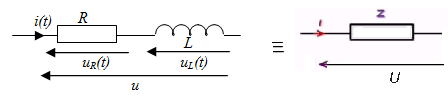
u(t) = uR(t) + uL(t)
U = Z.I UR = R.I UL = Lω.I
Construction de Fresnel :
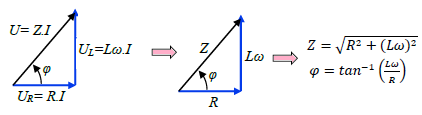
Tableau groupement en série
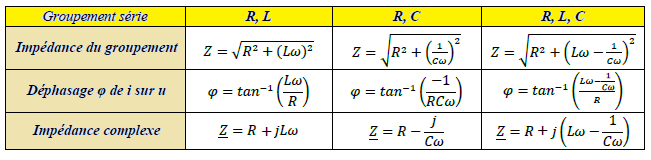
Association de dipôles en parallèle
Admittance: est l’inverse de l’impédance: Y=1/Z, on peut écrire : I = Y.U
Tableau ; Admittance des dipôles élémentaires

En parallèle, les admittances complexes s’additionnent :
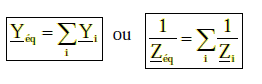
Groupement parallèle R, L
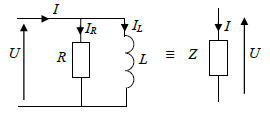
Construction de Fresnel

Tableau groupement en parallèle
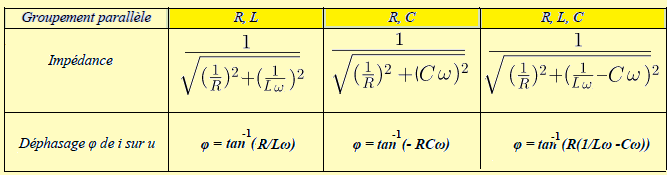
Puissances en alternatif
Puissances
La puissance électrique instantanée est le produit de la tension par le courant.
p(t) = U 2 sin ωt. I 2 sin (ωt – φ) = 2UIsin ωt. sin (ωt – φ)
- u (t) = U √2 sin ωt
- i(t) = I √2 sin (ωt – φ).
on utilise la relation trigonométrique: sin a .sin b =1/2[cos(a-b)+cos(a+b)]
p(t) = UIcos(ωt+φ-ωt )- U.I.cos (ωt+φ+ωt) = U.I.cosφ – U.I.cos (2ωt+φ)
Finalement: p(t) =U.I.cosφ – U.I.cos (2ωt+φ)
Puissance active
on appelle puissance active P la puissance moyenne de p(t)
P = <p(t)> = <U.I cos φ>- <U.I.cos (2ωt+φ)>
cos (2ωt+φ) est sinusoïdal donc sa valeur moyenne est nulle.
donc la puissance active est : P =U.I.cosφ
elle Correspond à une fourniture réelle d’énergie transmise au récepteur et convertible en chaleur ou en travail en tenant compte du déphasage entre la tension et le courant.. Elle est mesurée avec un wattmètre
- P: puissance active en W
- U: tension efficace en V
- I: intensité efficace en A
- φ: déphasage de u par rapport à i en rad.
Puissance réactive
Q = U.I.sin φ unité : le voltampère réactif (VAR).
Correspond à la puissance fictive qui caractérise l’échange d’énergie non utilisée pour fournir un travail.
Puissance apparente
S = U.I mesurée avec un voltmètre et un ampèremètre unité : le voltampère (VA).
Relation entre les puissances
Triangle des puissances
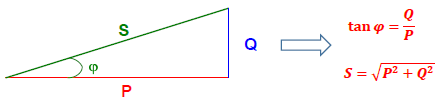
Ce triangle donne immédiatement les relations suivantes :
cos φ = P / S sin φ = Q / S tan φ = Q / P S² = P² + Q²
Puissances consommées par les dipôles passifs élémentaires
Résistance
pour une résistance le déphasage φ de u par rapport à i est nul alors sin φ= 0 donc Q = 0
une résistance ne consomme pas de puissance réactive
Bobine
on a un déphasage φ=+π/2 alors sin φ= 1 soit Q = UI= LωI²=U²/Lω avec ( I=U/Z)
la puissance active P= UI cosφ=0 , donc une bobine absorbe de la puissance réactive
Condensateur
on a φ=-π/2 alors sin φ= -1 soit Q = -UI =- U²Cω = -I² / Cω ) et la puissance active P= UI cosφ=0
donc un condensateur fournît de la puissance réactive
Tableau rassemble les Puissances consommées par les dipôles passifs élémentaires
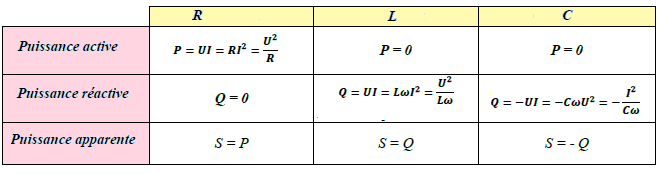
Théorème de Boucherot
Les puissances active et réactive absorbées par un groupement de dipôles sont respectivement égales à la somme des puissances actives et réactives absorbées par chaque élément du groupement.
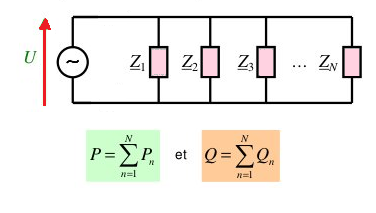
Importance du facteur de puissance
La tension U (230 V ) , imposée par le réseau, la puissance active P imposée par l’installation électrique à alimenter, on a la relation du courant I = P /U. cosφ
Plus votre installation comporte de moteurs asynchrones ( bobinage) plus le déphasage entre le courant et la tension devient élevé ( cos φ diminue) plus le courant devient fort I = P /U. cosφ et (Q = U.I.sin φ augmente) plus de consommation de la puissance réactive .cette puissance trop élevée sera facturée par le fournisseur d’énergie. Comment réduire la consommation de puissance réactive
la réponse il faut augmenter le facteur de puissance au minimum cos φ= 0,93 . c’est ce qu’on appelle relèvement du facteur de puissance. Un bon facteur de puissance c’est cos φ élevé proche de 1 ou tg φ faible proche de 0
Relèvement du facteur de puissance
Augmenter cos φ, donc réduire l’angle de déphasage. Pour se faire . il faut donc y ajouter en parallèle un condensateur.
Le condensateur est un composant permettant de déphaser de 90° en avance le courant i par
rapport à la tension u.
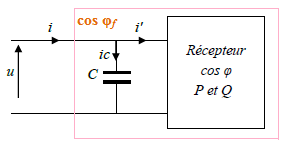
Notre but est de dimensionner le condensateur en fonction du facteur de puissance recherché cos φf
Lorsque le facteur de puissance augmente de cos φ à cos φf le déphasage diminue et la puissance réactive diminue de Q = P tan φ à Qf = P tan φf
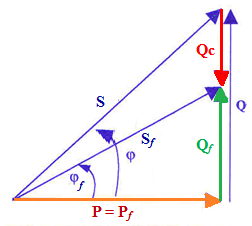
D’après la construction graphique, on a :
Qc + Q= Qf on déduit Qc= Qf – Q
on sait que :Q = P tan φ et Qf = P tan φf
donc on en déduit : Qc = P ( tan φf – tan φ )
La puissance réactive fournie par un condensateur est :
Qc = – U² C ω
donc – U² C ω = P ( tan φf – tan φ )
Finalement la valeur du condensateur est : C = P ( tan φ – tan φf )/U² ω
Réseau triphasé équilibré
Un système triphasé est un réseau à trois tensions [courants] sinusoïdales alternatives, de même fréquence, déphasées, les unes par rapport aux autres, d’un angle de 2π/3. 120°
On dit que le système est équilibré si les trois grandeurs sinusoïdales sont de même valeur efficace.
Tension simple
Tension simple: est la différence de potentiel entre une phase et le neutre. Nous les noterons : v1(t), v2(t) et v3(t)
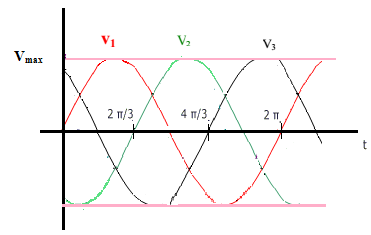
Les trois tensions simples sont :
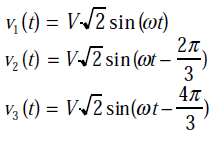
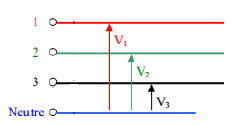
Représentation temporelle des tensions simples
Écriture des tensions simples en complexe
V1 = [V, 0°] V2 = [V, -120°] V3 = [V, -240°]
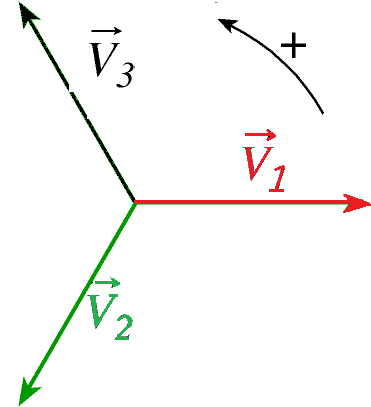
Vecteurs de Fresnel associés
Tension composée
Tension composée : est la différence de potentiel entre 2 phases. Nous les noterons : u12(t),u23(t) et u31(t).
Avec u12(t) = v1(t) – v2(t) u23(t)= v2(t) – v3(t) u31(t)= v3(t) – v1(t)
Les trois tensions composées sont:
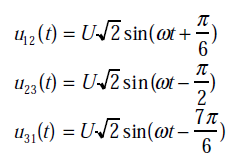
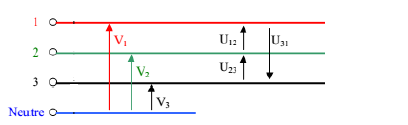
Représentation temporelle des tensions composées
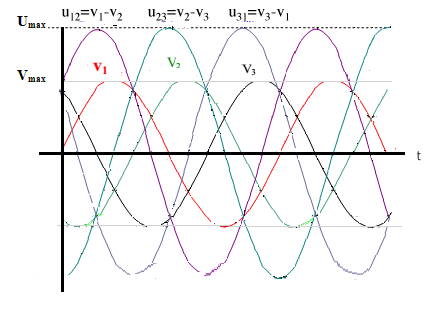
Écriture des tensions composées en complexe
U12 =V1 – V2 = [V√3, + 30°]
U23 =V2 – V3 = [V√3, – 90°]
U31 =V3 – V1 = [V√3, + 150°]
Vecteurs de Fresnel associés
Représentation vectorielle de FRESNEL des tensions :
Relation entre U et V
U = 2V cos 30 soit U = 2V√3/2 Finalement : U = V√3
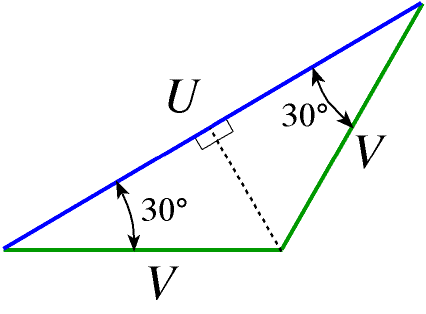
Propriétés importantes :
- La somme de trois grandeurs formant un système triphasé équilibré est nulle : V1+V2+V3=0
- La relation qui existe entre la valeur efficace V et U U= √3.V
Récepteurs triphasés équilibrés
Récepteurs triphasés : ce sont des récepteurs constitués de trois dipôles d’impédance Z.
Equilibré : si Z1 = Z2 = Z3 = Z .
Courant par phase : c’est le courant qui traverse les éléments Z du récepteur triphasé. Symbole : J
Courants en ligne : c’est le courant dans les fils du réseau triphasé. Symbole : I
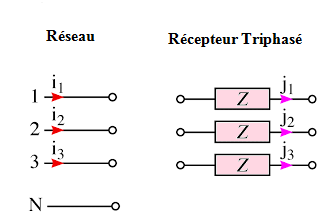
On peut relier le réseau et le récepteur de deux façons différentes : en étoile ou en triangle.
Couplage étoile
Montage :
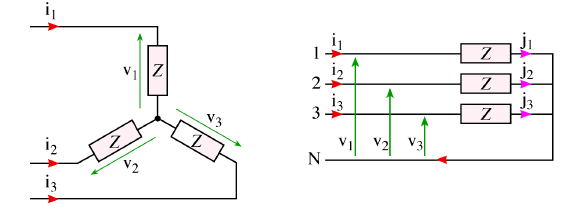
Les deux branchement sont les mêmes seulement représentés de deux façons différentes
Puisque les impédances sont identiques donc i1 + i2 + i3 = 0, alors iN = 0. le courant dans le fil neutre est nul. donc le fil neutre pas nécessaire.
le fil neutre ne sert à rien pour un système triphasé équilibré, .
Relations entre les courants :
On remarque que les courants en ligne sont égaux aux courants par phase.
i1 = j1 ; i2 = j2 ; i3 = j3
De plus puisque la charge et le réseau sont équilibrés, donc : I1 = I2 = I3 = I = J
A retenir le couplage étoile : I = J
Couplage triangle
Montage

Les deux branchement sont identiques seulement représentés de deux façons différentes
Les courants qui circulent dans les impédances Z sont différents des courants de ligne
J12 est généré par La tension U12
J23 est généré par La tension U23
J31est généré par La tension U31
Puisque les impédances sont identiques donc i1 + i2 + i3 = 0 et j12 + j23 + j31 = 0
En couplage triangle le fil neutre n’est pas nécessaire.
Relations entre les courants :
- i2 = j23 – j12 => I2 = J23 – J12
- i1 = j12 – j31 => I1 = J12 – J31
- i3 = j31 – j23 => I3 = J31 – J23
Le système triphasé est équilibré donc : I1 = I2 = I3 = I et J1 = J2 = J3 = J.
la relation entre I et J est : I = √3 J
Récepteurs triphasés déséquilibrés
Un récepteur est non équilibré si ses trois impédances Z1, Z2 et Z3 sont différentes, que ce soit couplé en étoile ou en triangle
Couplage étoile avec neutre
La somme des trois courants en ligne n’est plus nécessairement nulle, donc on a un courant qui circule dans le conducteur de neutre
Couplage triangle
Puisque le système est déséquilibré alors la relation I =√3 J n’est plus valable car .
Puissances en triphasé
Théorème de Boucherot
Les puissances active et réactive absorbées par un groupement de dipôles sont respectivement égales à la somme des puissances actives et réactives absorbées par chaque élément du groupement
On a donc P = P1+P2+P3 et Q = Q1+Q2+Q3
Charge triphasée déséquilibrée
En cas de charge déséquilibrée, tensions et courants sont déphasées de φ1, φ2 ou φ3 suivant les phases.
La puissance active est :P = V1.I1.cos φ1 + V2.I2.cos φ2 + V3.I3.cos φ3
Et la puissance réactive s’écrit alors : Q = V1.I1. sin φ1 + V2.I2. sin φ2 + V3.I3. sin φ3
Charge triphasée équilibrée
Si la charge est équilibrée, les trois impédances sont identiques, donc :
φ1 = φ2 = φ3 = φ ; V1 = V2 = V3 = V et I1 = I2 = I3 = I.
Pour un récepteur équilibré : P1=P2=P3 alors P = P1+P2+P3=3.P1
et Q1=Q2=Q3 donc Q=Q1+Q2+Q3=3.Q1
La puissance active a pour expression : P = 3.V.I.cos φ
La puissance réactive est : Q = 3.V.I.sin φ.
On peut exprimer la puissance active et la puissance réactive en fonction tension composée U
P = √3.U.I.cos φ Q = √3.U.I.sin φ S = √3.U.I
Mesure de puissance en triphasé
Mesure de la puissance active P
Ligne à 4 fils et circuit est équilibré
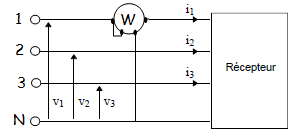
Lorsque le récepteur est équilibré, un seul wattmètre suffit pour mesurer la puissance active absorbée.
, c’est à dire on mesurer la puissance consommée par une phase et de multiplier par trois.
La puissance absorbée par le récepteur triphasé équilibré est P = 3P1
Ligne à 4 fils et circuit déséquilibré
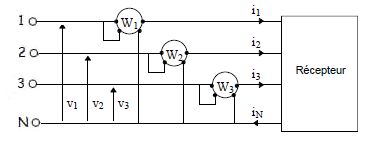
Il faut mesurer les puissances consommées par les trois phases et additionner.
Trois wattmètres sont nécessaires pour mesure la puissance active :
P = P1N + P2N + P3N
Ligne à 3 fils
Circuit équilibré ou déséquilibré
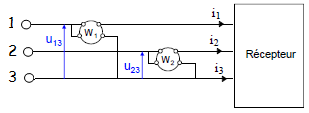
Pour un système déséquilibré ou un système équilibré dont le neutre n’est
pas accessible, on mesure la puissance active à l’aide de deux wattmètres.
On détermine la puissance active absorbée à l’aide de la relation : P = P1 + P2
Amélioration du facteur de puissance « cos φ «
Un facteur de puissance faible entraine :
- Une puissance apparente 𝑺 plus élevée
- Une consommation de l’énergie réactive 𝑸
- Une consommation d’énergie plus importante
Moyen utilisé pour relever le facteur de puissance : (Augmenter cos φ)
L’addition de condensateurs permet de réduire l’énergie réactive, on utilise une batterie de condensateurs que l’on raccorde aux bornes du récepteur ou de l’installation à compenser.
On utilise le montage triangle dans les réseaux BT (basse tension), et le montage étoile dans les réseaux HT (haute tension)
Relèvement du facteur de puissance
Un bon facteur de puissance est que le cos φ proche de 1, minimum cos φ= 0,93
Couplage des condensateurs en triangle :
U:Tension aux bornes d’un condensateur
Puissance réactive absorbée par un condensateur : QC1 = – CωU2
Puissance réactive absorbée par les trois condensateurs : QC = 3QC1 = -3CωU2
Détermination de la capacité
On calcule la capacité du condensateur de la manière suivante:
QC = -3C.ω.U2 = Q’- Q
-3C.ω.U2 = P.tg φ’ – P.tg φ
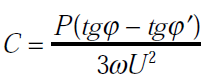
Couplage des condensateurs en étoile:
En utilisant le même raisonnement que précédemment, on montre que la capacité du condensateur est :