Lois de Probabilités : Cours et Exercices Corrigés

Bienvenue dans le cours de : Lois de probabilité pour le terminale. vous trouverez les exercices ( exemples ) corrigés à la fin du cours.

Variable aléatoire discrète

Définition

Lorsque l’on associe à chaque éventualité d’un univers Ω d’une expérience aléatoire un nombre réel, on dit que l’on définit une variable aléatoire sur Ω

La variable aléatoire X est à valeurs x₁,x₂, …, x_n on dit que X est une variable aléatoire discrète

Exemple :

Une urne contient 6 boules jaunes, 3 boules Noirs et 1 boule blanche On prend une boule au hasard.

Si elle est blanche, on gagne 3 euros : B est l’événement « la boule est blanche « .
Si elle est Noire, on gagne 1euro : N est l’événement « la boule est Noir
Si elle est jaune, on ne gagne rien : J est l’événement « la boule est jaune « .

Couleur boule	B	N	J
X	3	1

On a l’univers Ω ={B, N, J} , et la variable X, appelée variable aléatoire, associée au nombre d’euro que l’on gagne, prend les valeurs 0 , 1 ou 3 : on note X(Ω) ={0 , 1 , 3}

Loi de probabilité de variable aléatoire

La probabilité de l’évènement « X = x_i » est la probabilité de l’évènement formé de toutes les issues associées au nombre x_i

La donnée de toutes les probabilités P( X= x_i ) est la loi de probabilité discrète de la variable aléatoire X :

x_i	x₁	x₂	…	…	x_n	TOTAL
P( X= x_i )	p₁	p₂			p_n	1

On reprend l’énoncé de l’exemple précédent :

La probabilité de gagner 3 euros , notée P( X= 3 ) = $\frac{1}{10}$
La probabilité de gagner 1euro, notée P( X= 1 ) = $\frac{3}{10}$
La probabilité de gagner 0 euro , notée P( X= ) = $\frac{6}{10}$

On définit ainsi une loi de probabilité de la variable aléatoire X :

Valeurs de x_i		1	3
P( X= x_i )	0,6	0,3	0,1

P( X= ) +P( X= 1 ) +P( X= 3 ) =1

Espérance mathématique d’une variable aléatoire

Définition :

L’espérance mathématique d’une variable aléatoire X qui suit une loi de probabilité est la moyenne : E(X) = p₁ × x₁+ p₂ × x₂+ p₃ × x₃+…+p_n×x_n

On l’écrit aussi sous forme : E(X)= $\sum_{i=1}^{n}p_{i}\times x_{i}$

L’espérance de cette loi de probabilité de l’exemple précédent est :

Voir aussi: Etat d'équilibre D'Un Système Chimique : Cours & Exercices

E(X) = 0.6 × 0 + 0.3 × 1 + 0.1 × 3=0.6

Variance et écart type d’une variable aléatoire discrète

La variance d’une variable aléatoire discrète X, notée V(X) est le nombre réel positif : V(X)= $\sum_{i=1}^{n}p_{i}\times \left (x _{i} \right-E(X) )^{2}$

L’écart type est la racine carrée de la variance : σ = $\sqrt{V(X)}$

Autre formule possible pour calculer la variance : V(X)= $\sum_{i=1}^{n}p_{i}\times x _{i}^{2}-(E(X))^{2}$

Loi binomiale

Épreuve de Bernoulli

Définition :

Une épreuve de Bernoulli est une expérience aléatoire à deux issues : (« succès » ou « échec »)

Loi de Bernoulli

Définition

Une loi de Bernoulli est une loi de probabilité qui suit le schéma suivant :

la probabilité d’obtenir un succès est égale à p
la probabilité d’obtenir un échec est égale à q= 1 – p
- - p est appelé le paramètre de la loi de Bernoulli

Exemples :

On tire au hasard une boule d’une urne qui contient 10 boules, 3 sont blanches et 7 sont noires.

On considère comme succès « tirer une boule blanche » et échec « tirer une boule noire ».

la probabilité d’obtenir un succès est p= $\frac{3}{10}$ et la probabilité d’obtenir un échec est q= $\frac{7}{10}$ ( q=1-p)

Au succès, on peut associer le nombre 1
A l’échec on peut associer le nombre 0.

Pendant un tirage La variable aléatoire X « nombre de succès » peut prendre soit :

X=1 si la boule tirée est blanche
X=0 si la boule tirée est noire

La loi de probabilité de X est :

x_i		1
P( X= x_i )	q= $\frac{7}{10}$	p= $\frac{3}{10}$

On dit que La variable aléatoire X suit une loi de Bernoulli de paramètre p

Schéma de Bernoulli

Définition :

Un schéma de Bernoulli est la répétition de n épreuves de Bernoulli identiques et indépendantes pour lesquelles la probabilité du succès est p On considère un schéma de n épreuves de Bernoulli représentée par un arbre et k est un entier compris entre 0 et n.

L’entier $\binom{n}{k}$ est le nombre de chemins de l’arbre réalisant k succès parmi n épreuve.

Exemple :

Une urne contient 10 boules : 6 rouges et 4 boules blanches. On prélève au hasard successivement, avec remise, 4 boules de l’urne. X désigne le nombre de boules rouges obtenues à l’issue des 3 tirages. Quelle est la loi de probabilité de la variable aléatoire X ?

Voir aussi: Transformations associées à des réactions acido-basiques en solution aqueuse

Solution : Un tirage de 4 boules consiste en 3 épreuves, identiques et indépendantes (puisque les prélèvements sont avec remise). Chaque épreuve a deux issues possibles : « succès » S : la boule est blanche avec la probabilité p=0.4 « échec » $\bar{S}$ : la boule est rouge avec la probabilité q=0.6

La variable aléatoire X « nombre de succès » suit la loi B(n,p) de paramètres n =3 et p=0.4

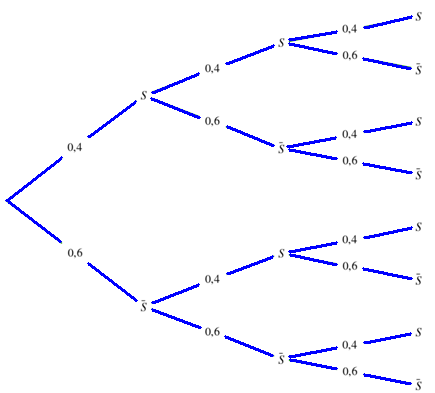
La loi de probabilité de X est résumée dans le tableau:

x_i		1	2	3	Total
P( X= x_i )	1x0,4x0,6³	3x0,4¹x0,6²	3x0,4²x0,6¹	1x0,4³x0,6	1

X : la variable aléatoire qui donne le nombre de succès.
p : la probabilité du succès
q=1-p probabilité de l’échec .

Alors X suit la loi binomiale de paramètres n et p et pour tout entier k compris entre 0 et n , on a : la formule générale: $P(X=k)=\binom{n}{k}\times p^{k}\times q^{n-k}$

Le coefficient binomial $\binom{n}{k}=\frac{n!}{k!(n-k)!}$ est le nombre entier de chemins de l’arbre réalisant k succès parmi n

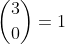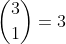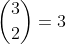
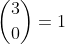
$\binom{3}{0}=1$ ; $\binom{3}{1}=3$ ; $\binom{3}{2}=3$ $\binom{3}{0}=1$

Les coefficients binomiaux 1 3 3 1 indiquent le nombre de chemins de l’arbre réalisant k succès.

Exemple

On a mis dans une urne 100 boules : 25 bleues et 75 rouges.
- On appelle succès l’évènement : « obtenir une boule bleue ».
- Une partie de jeu consiste à tirer successivement 7 boules avec remise.
- On appelle la variable aléatoire qui donne le nombre de boules bleues obtenues au cours d’une partie.

Quelle est la loi de probabilité suivie par X ?
Quelle est la probabilité d’avoir 5 boules bleues ?

Solution :

Il y a n=7 épreuves de Bernoulli identiques et indépendantes, avec p=0,25 probabilité de succès et q=0,75 probabilité d’échec . Donc la variable aléatoire suit la loi binomiale B(7;0,25)
$P(X=5)=\binom{7}{5}\times 0,25^{5}\times 0,75^{2}$

Si vous avez des remarques ou des questions à propos du cours : Lois de probabilités , laissez les dans les commentaires

80%

Awesome

Design