Cours avec des exercices corrigés : intégrale d’une fonction pour le terminale.
Notion d’intégrale
Le but de l’intégration est de calculer la surface et le volume délimité par une courbe et l’axe des abscisses.
INTÉGRALE D’UNE FONCTION CONTINUE
1 DÉFINITION
Soit f une fonction continue sur un intervalle [a; b] et F une primitive de la fonction f sur l’intervalle [a; b]
le nombre réel F(b) −F(a) s’appelle l’intégrale de f entre a et b qu’on note :
f(x)dx = F(b) −F(a)
Et on lit « intégrale de a à b de f(x)dx.
On note aussi = F(b) −F(a)
Donc f(x)dx =
=F(b) −F(a)
2 Propriété :
Soit f et g deux fonctions continues sur I et a, b et c trois réels de I et k nombre réel Alors :
Relation de Chasles
f(x)dx =
f(x)dx+
f(x)dx
Linéarité :
( f(x)+g(x) ) dx=
f(x)dx+
f(x)dx
K f(x) dx = k *
f(x)dx
Permutation des bornes
f(x)dx= –
f(x)dx
f(x)dx=
f(x)dx –
f(x)dx
f(x)dx=0
Inégalité :
- si f ≥ 0 Sur [a , b] et a ≤ b alors
f(x)dx ≥ 0
- si f(x) ≤ g(x) et a ≤ b (∀ x ∈ [a;b]) alors
f(x)dx ≤
g(x) dx
Sur un intervalle [a, b] avec a<b la fonction est comprise entre m et M ; on a m ≤ f(x) ≤ M
On intègre on a alors m dx ≤
f(x)dx ≤
M dx
C’est à dire m(b – a) ≤ f(x)dx ≤ M(b – a)
La valeur moyenne
Définition et théorème
Soit f fonction continue sur I et a, b deux nombres de I tel que a < b Alors :
Il existe au moins une valeur c ∈ [a;b] tel que f(c) =
f(x)dx
La valeur moyenne de f est égal à:
f(x)dx
3 Intégration par parties
Soit f et g deux fonctions dérivable sur [a; b] tel que f ‘ et g’ sont continues sur [a;b]
On a
Toute notre étude sera dans un repère orthogonal
Unité d’aire
On appelle unité d’aire u.a l’aire d’un rectangle OIKJ
1u.a =
4 Définition :
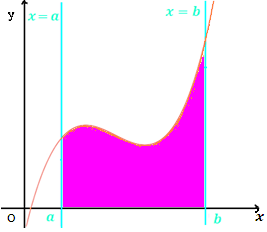
Soit f une fonction continue et positive sur un intervalle [a ; b].
Soit A aire la surface délimitée par :
- la courbe C représentative de la fonction f,
- l’axe des abscisses OX
- les droites d’équations x=a et x=b
Intégrale de f sur [a ;b] : mesure de l’aire en u.a. du domaine situé sous la courbe Cf .
On la note : A= f(x)dx
si f ≥0 Sur [a , b] et a ≤ b alors f(x)dx ≥ 0
Si f est positif sur [a ;b] alors A=f(x)dx ≥ 0 exprimée en u.a
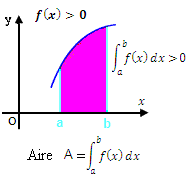
Exemples
1. Calculer l’intégral de f(x) = x2 dans l’intervalle [0 , 2]
Solution
f(x) dx = F(b) −F(a)
x2 dx=
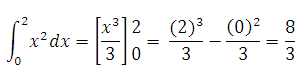
2- . Déterminer l’intégral de f(x) = ex dans l’intervalle [1 , 5]
Solution
f(x)dx =
ex dx= = e5-e1
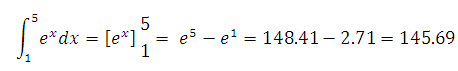
3-Déterminer l’aire de f(x) = dans l’intervalle [0 , 9]
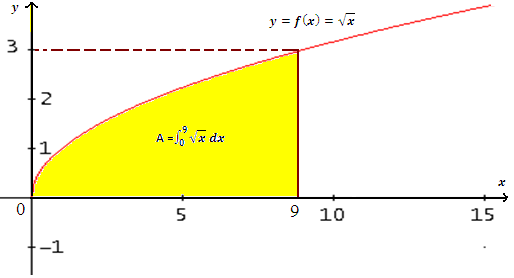
Solution
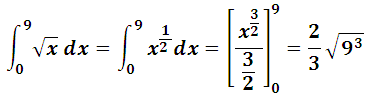
Intégrale d’une fonction continue négative
si f ≤ 0 Sur [a , b] et a ≤ b alors f(x) dx ≤ 0
Aire A= –f(x)dx
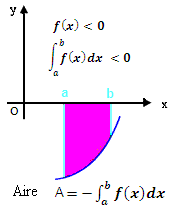
L’aire est exprimé positivement donc A= |f(x)| dx exprimée en u.a.,
Exemple :
Calculer l’Aire de f(x) = -4 entre x = -2 et x = 3
La courbe de f(x) = -4
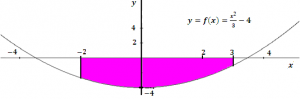
f(x)<0 sur l’intervalle [-2 , 3] donc :
Aire A= – f(x) dx
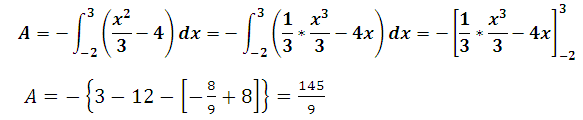
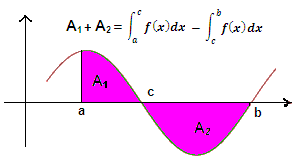
Intégrale d’une fonction continue de signe quelconque
Exemple
Calculer l’Aire de f(x)= 3x2+7x-6 entre x=-4 et x=2
A= 3x2+7x-6 dx = A1+A2+A3
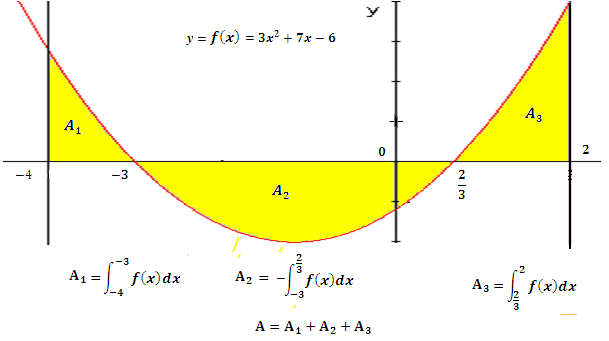
Sur l’intervalle [-4 , -3] f(x)>0 donc A1= 3x2+7x-6 dx
Sur l’intervalle [-3 , ] f(x) <0 donc A2= –
3x2+7x-6 dx
Sur l’intervalle [ , 2] f(x)>0 donc A3 =
3x2+7x-6 dx
Alors l’aire de la fonction entre x=-4 et x=2 est:
A= 3x2+7x-6 dx = A1+A2+A3
A= 3x2+7x-6 dx –
3x2+7x-6 dx +
3x2+7x-6 dx
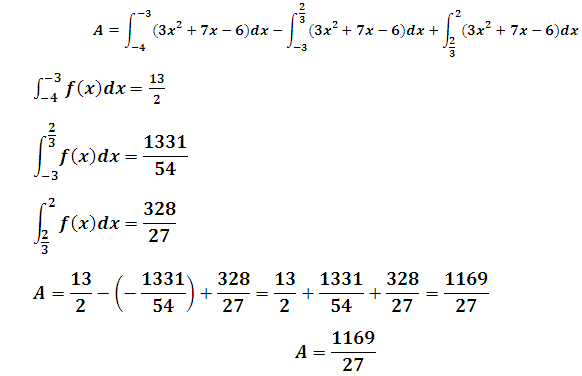
Aire limitée par deux courbes
5 Théorème
Soit f et g sont des fonctions continues sur l’intervalle[a ;b]
L’aire de la surface délimitée par les 2 courbes f et g , et les droites d’équations respectivement x = a et x = b est égale à :
Exemple
Calculer l’aire délimitée par les 2 courbes f et g entre x=0 et x= 3
g(x)=8 – x2 et f(x)= x2
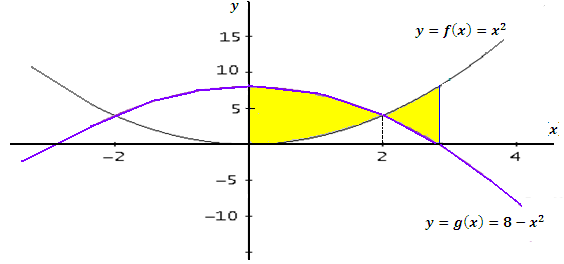
l’aire délimitée par les 2 courbes f et g entre x=0 et x= 3 est égal
| f(x)-g(x)| dx
Sur l’intervalle [0 , 2] g(x) > f(x) donc :
A1= [ g(x)- f(x)] dx=
(8 – 2x2) dx
Sur l’intervalle [2 , 3] f(x)> g(x) donc :
A2= [ f(x)-g(x)] dx =
(2x2– 8) dx
A1+A2 = (8 – 2x2) dx +
(2x2– 8) dx
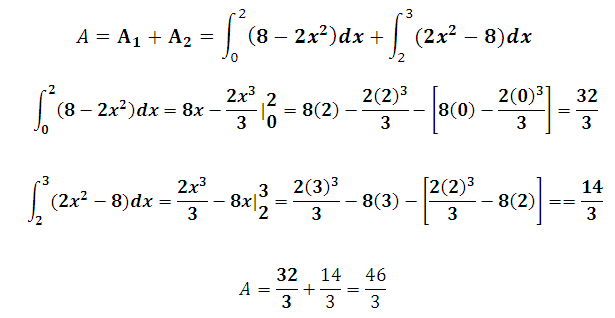
CALCULS DE VOLUME
L’espace est muni d’un repère orthogonal
Unité de volume est noté par u.v. égal à
6 Théorème
L’espace est muni d’un repère orthogonal
Soit f fonction continue sur l’intervalle [a; b] avec ( a < b )
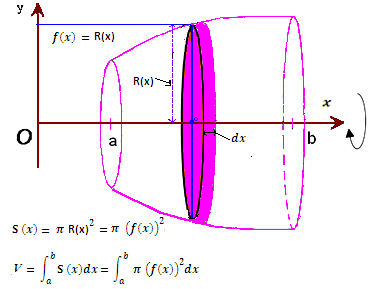
le volume du solide est généré par la révolution autour de l’axe Ox de la courbe
y = f (x) comprise entre x = a et x = b et égal à :
V=
Exemple
1. calculer le volume du solide de révolution que se forme autour de Ox de la fonction f(x)=2 sur l’intervalle [-2 , 3]
Solution:
V= S (x)dx =
π ( f(x))2 dx=
π ( 2)2 dx= 4π
dx=
4π = 4π(3-(-2))= 20π
2. calculer le volume du solide de révolution que se forme autour de Ox de la fonction f(x)= x sur l’intervalle [0 , 4]
Solution:
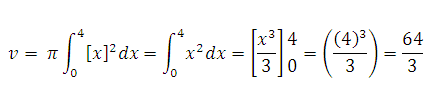
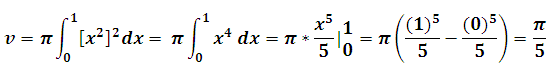
En a arrivé à la fin du cours d’intégrale d’une fonction, si vous avez des questions, laissez un commentaire.
- Design







